【題目】已知
是定義在
上的偶函數，且滿足
，若當
時，
，則函數
在區間
上零點的個數為（ ）
A. 2017 B. 2018 C. 4034 D. 4036
【答案】D
【解析】試題分析：函數g（x）=f（x）﹣e﹣|x|在區間[﹣2018，2018]上零點的個數函數的圖象
與y=e﹣|x|的圖象交點個數．
是定義在
上的偶函數，由
得f（x）是周期為2的偶函數，根據當x∈[0，1]時，，作出y=f（x）與
圖象,結合圖象即可．
詳解：函數g（x）=f（x）﹣e﹣|x|在區間[﹣2018，2018]上零點的個數函數的圖象與y=e﹣|x|的圖象交點個數．
由是定義在上的偶函數，且滿足，即f（﹣x）=f（x）．
又∵，f（x）是周期為2的偶函數．
∵當x∈[0，1]時，，
作出y=f（x）與圖象如下圖，
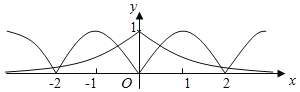
可知每個周期內有兩個交點，所以函數g（x）=f（x）﹣e﹣|x|在區間[﹣2018，2018]上零點的個數為2018×2=4036．
故選：D．
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，已知曲線
的參數方程為
（
為參數），以原點
為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
.
（1）求曲線的普通方程與的直角坐標方程；
（2）判斷曲線
是否相交，若相交，求出相交弦長.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，傾斜角為
的直線
的參數方程為
．以坐標原點為極點，以
軸的正半軸為極軸，建立極坐標系，曲線
的極坐標方程是
．
（1）寫出直線的普通方程和曲線的直角坐標方程；
（2）已知點
．若點
的極坐標為
，直線經過點且與曲線相交于
，
兩點，求，兩點間的距離
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設集合A={x|x2-3x+2=0}，B={x|x2+（a-1）x+a2-5=0}．
（1）若A∩B={2}，求實數a的值；
（2）若A∪B=A，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為考查某種疫苗預防疾病的效果，進行動物實驗，得到統計數據如下：
未發病 | 發病 | 總計 | |
未注射疫苗 | 20 |
|
|
注射疫苗 | 30 |
|
|
總計 | 50 | 50 | 100 |
現從所有試驗動物中任取一只，取到“注射疫苗”動物的概率為
.
（1）求
列聯表中的數據
，
，
，
的值；
（2）判斷疫苗是否有效？
（3）能夠有多大把握認為疫苗有效？
（參考公式
，
）
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數f（x）滿足條件f（0）＝1，及f（x+1）﹣f（x）＝2x．
（1）求函數f（x）的解析式；
（2）在區間[﹣1，1]上，y＝f（x）的圖象恒在y＝2x+m的圖象上方，試確定實數m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，已知點P是平行四邊形ABCD所在平面外一點，M、N分別是AB、PC的中點．
（1）求證：MN∥平面PAD；
（2）在PB上確定一個點Q，使平面MNQ∥平面PAD.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
