
已知雙曲線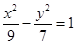 與橢圓
與橢圓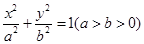 有相同的焦點,點
有相同的焦點,點 、
、 分別是橢圓的右、右頂點,若橢圓經過點
分別是橢圓的右、右頂點,若橢圓經過點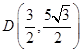 .
.
(1)求橢圓的方程;
(2)已知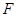 是橢圓的右焦點,以
是橢圓的右焦點,以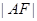 為直徑的圓記為
為直徑的圓記為 ,過點
,過點 引圓
引圓 的切線,求此切線的方程;
的切線,求此切線的方程;
(3)設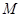 為直線
為直線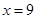 上的點,
上的點,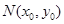 是圓
是圓 上的任意一點,是否存在定點
上的任意一點,是否存在定點 ,使得
,使得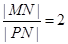 ?若存在,求出定點
?若存在,求出定點 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
(Ⅰ)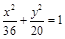 .(Ⅱ)
.(Ⅱ) .(Ⅲ)存在定點
.(Ⅲ)存在定點
解析試題分析:(Ⅰ)依題意,
 ,
,
所以橢圓的方程為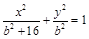 ,
,
代入D點坐標,解得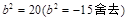 ,由此得
,由此得 ,
,
所以橢圓的方程為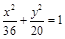 . (4分)
. (4分)
(Ⅱ)由(Ⅰ)知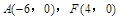 ,故圓
,故圓 的方程為
的方程為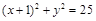 ,
,
則由 知,點
知,點 在圓
在圓 上,
上,
因為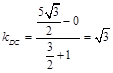 ,所以切線的斜率為
,所以切線的斜率為 ,
,
故所求切線的方程為 ,
,
即 . (8分)
. (8分)
(Ⅲ)設 ,假設存在點
,假設存在點 滿足題意,
滿足題意,
則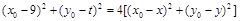 ,
,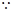 點
點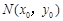 在圓C:
在圓C: 上,
上,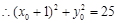 ,
,
化簡得 ,
,
因為該式對任意的 恒成立,則
恒成立,則 解得
解得
故存在定點 對于直線
對于直線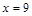 上的點
上的點 及圓
及圓 上的任意一點
上的任意一點 使得
使得 成立. (12分)
成立. (12分)
考點:本題考查了橢圓方程及直線與圓的位置關系
點評:從近幾年課標地區的高考命題來看,解析幾何綜合題主要考查直線和圓錐曲線的位置關系以及范圍、最值、定點、定值、存在性等問題,直線與多種曲線的位置關系的綜合問題將會逐步成為今后命題的熱點,尤其是把直線和圓的位置關系同本部分知識的結合,將逐步成為今后命題的一種趨勢.近幾年高考題中經常出現了以函數、平面向量、導數、數列、不等式、平面幾何、數學思想方法等知識為背景,綜合考查運用圓錐曲線的有關知識分析問題、解決問題的能力,試題風格每年都有所創新,但總體穩定.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
已知平面內一動點 到點
到點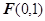 的距離與點
的距離與點 到
到 軸的距離的差等于1.(I)求動點
軸的距離的差等于1.(I)求動點 的軌跡
的軌跡 的方程;(II)過點
的方程;(II)過點 作兩條斜率存在且互相垂直的直線
作兩條斜率存在且互相垂直的直線 ,設
,設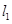 與軌跡
與軌跡 相交于點
相交于點 ,
, 與軌跡
與軌跡 相交于點
相交于點 ,求
,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓 :
: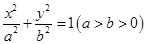 的一個焦點為
的一個焦點為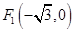 且過點
且過點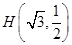 .
.
(Ⅰ)求橢圓E的方程;
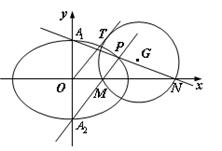
(Ⅱ)設橢圓E的上下頂點分別為A1,A2,P是橢圓上異于A1,A2的任一點,直線PA1,PA2分別交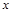 軸于點N,M,若直線OT與過點M,N的圓G相切,切點為T.
軸于點N,M,若直線OT與過點M,N的圓G相切,切點為T.
證明:線段OT的長為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知橢圓 :
: ,左、右兩個焦點分別為
,左、右兩個焦點分別為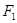 、
、 ,上頂點
,上頂點 ,
,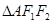 為正三角形且周長為6.
為正三角形且周長為6.
(1)求橢圓 的標準方程及離心率;
的標準方程及離心率;
(2) 為坐標原點,
為坐標原點, 是直線
是直線 上的一個動點,求
上的一個動點,求 的最小值,并求出此時點
的最小值,并求出此時點 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設橢圓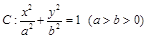 的左、右焦點分別為
的左、右焦點分別為 ,上頂點為
,上頂點為 ,離心率為
,離心率為 , 在
, 在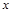 軸負半軸上有一點
軸負半軸上有一點 ,且
,且
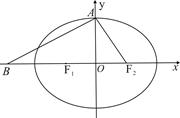
(1)若過 三點的圓 恰好與直線
三點的圓 恰好與直線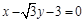 相切,求橢圓C的方程;
相切,求橢圓C的方程;
(2)在(1)的條件下,過右焦點 作斜率為
作斜率為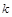 的直線
的直線 與橢圓C交于
與橢圓C交于 兩點,在
兩點,在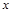 軸上是否存在點
軸上是否存在點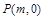 ,使得以
,使得以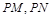 為鄰邊的平行四邊形是菱形,如果存在,求出
為鄰邊的平行四邊形是菱形,如果存在,求出 的取值范圍;如果不存在,說明理由.
的取值范圍;如果不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,設拋物線 (
( )的準線與
)的準線與 軸交于
軸交于 ,焦點為
,焦點為 ;以
;以 、
、 為焦點,離心率
為焦點,離心率 的橢圓
的橢圓 與拋物線
與拋物線 在
在 軸上方的一個交點為
軸上方的一個交點為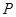 .
.
(1)當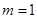 時,求橢圓的方程;
時,求橢圓的方程;
(2)在(1)的條件下,直線 經過橢圓
經過橢圓 的右焦點
的右焦點 ,與拋物線
,與拋物線 交于
交于 、
、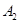 ,如果以線段
,如果以線段 為直徑作圓,試判斷點
為直徑作圓,試判斷點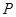 與圓的位置關系,并說明理由;
與圓的位置關系,并說明理由;
(3)是否存在實數 ,使得
,使得 的邊長是連續的自然數,若存在,求出這樣的實數
的邊長是連續的自然數,若存在,求出這樣的實數 ;若不存在,請說明理由.
;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com