
【題目】各項均為非負整數的數列{an}同時滿足下列條件: ①a1=m(m∈N*);②an≤n﹣1(n≥2);③n是a1+a2+…+an的因數(n≥1).
(Ⅰ)當m=5時,寫出數列{an}的前五項;
(Ⅱ)若數列{an}的前三項互不相等,且n≥3時,an為常數,求m的值;
(Ⅲ)求證:對任意正整數m,存在正整數M,使得n≥M時,an為常數.
【答案】解:(Ⅰ) m=5時,數列{an}的前五項分別為:5,1,0,2,2.
(Ⅱ)∵0≤an≤n﹣1,∴0≤a2≤1,0≤a3≤2,
又數列{an}的前3項互不相等,
⑴當a2=0時,
若a3=1,則a3=a4=a5=…=1,
且對n≥3, ![]() 都為整數,∴m=2;
都為整數,∴m=2;
若a3=2,則a3=a4=a5=…=2,
且對n≥3, ![]() 都為整數,∴m=4;
都為整數,∴m=4;
⑵當a2=1時,
若a3=0,則a3=a4=a5=…=0,
且對n≥3, ![]() 都為整數,∴m=﹣1,不符合題意;
都為整數,∴m=﹣1,不符合題意;
若a3=2,則a3=a4=a5=…=2,
且對n≥3, ![]() 都為整數,∴m=3;
都為整數,∴m=3;
綜上,m的值為2,3,4.
(Ⅲ)證明:對于n≥1,令Sn=a1+a2+…+an,
則 ![]() .
.
又對每一個n, ![]() 都為正整數,∴
都為正整數,∴ ![]() ,其中“<”至多出現m﹣1個.
,其中“<”至多出現m﹣1個.
故存在正整數M>m,當n>M時,必有 ![]() 成立.
成立.
當 ![]() 時,則
時,則 ![]() .
.
從而 ![]() .
.
由題設知 ![]() ,又
,又 ![]() 及an+1均為整數,
及an+1均為整數,
∴ ![]() =an+1=
=an+1= ![]() ,故
,故 ![]() =常數.
=常數.
從而 ![]() =常數.
=常數.
故存在正整數M,使得n≥M時,an為常數
【解析】(Ⅰ)當m=5時,寫出數列{an}的前五項;(Ⅱ)對a2、a3分類取值,再結合各項均為非負整數列式求m的值;(Ⅲ)令Sn=a1+a2+…+an,則 ![]() .進一步推得存在正整數M>m,當n>M時,必有
.進一步推得存在正整數M>m,當n>M時,必有 ![]() 成立.再由
成立.再由 ![]() 成立證明an為常數.
成立證明an為常數.
【考點精析】認真審題,首先需要了解數列的前n項和(數列{an}的前n項和sn與通項an的關系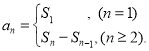 ).
).


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】設![]() 的對邊分別為
的對邊分別為![]() 且
且![]() 為銳角,問:(1)證明: B - A =
為銳角,問:(1)證明: B - A = ![]() ,(2)求 sin A + sin C 的取值范圍
,(2)求 sin A + sin C 的取值范圍
(1)(1)證明:![]()
(2)(2)求![]() 的取值范圍
的取值范圍
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列函數中,同時滿足兩個條件“①x∈R,f( ![]() +X)+f(
+X)+f( ![]() -X)=0;②當﹣
-X)=0;②當﹣ ![]() <x<
<x< ![]() 時,f′(x)>0”的一個函數是( )
時,f′(x)>0”的一個函數是( )
A.f(x)=sin(2x+ ![]() )
)
B.f(x)=cos(2x+ ![]() )
)
C.f(x)=sin(2x﹣ ![]() )
)
D.f(x)=cos(2x﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位附近只有甲,乙兩個臨時停車場,它們各有50個車位,為了方便市民停車,某互聯網停車公司對這兩個停車場在工作日某些固定時刻的剩余停車位進行記錄,如下表:
時間 | 8點 | 10點 | 12點 | 14點 | 16點 | 18點 |
停車場甲 | 10 | 3 | 12 | 6 | 12 | 17 |
停車場乙 | 13 | 4 | 3 | 2 | 6 | 19 |
如果表中某一時刻停車場剩余停車位數低于總車位數的10%,那么當車主驅車抵達單位附近時,該公司將會向車主發出停車場飽和警報.
(Ⅰ)假設某車主在以上六個時刻抵達單位附近的可能性相同,求他收到甲停車場飽和警報的概率;
(Ⅱ)從這六個時刻中任選一個時刻,求甲停車場比乙停車場剩余車位數少的概率;
(Ⅲ)當停車場乙發出飽和警報時,求停車場甲也發出飽和警報的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某市的中學生中隨機調查了部分男生,獲得了他們的身高數據,整理得到如下頻率分布直方圖. 
(Ⅰ)求a的值;
(Ⅱ)假設同組中的每個數據用該組區間的中點值代替,估計該市中學生中的全體男生的平均身高;
(Ⅲ)從該市的中學生中隨機抽取一名男生,根據直方圖中的信息,估計其身高在180cm 以上的概率.若從全市中學的男生(人數眾多)中隨機抽取3人,用X表示身高在180cm以上的男生人數,求隨機變量X的分布列和數學期望EX.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(ax﹣1)lnx+ ![]() . (Ⅰ)若a=2,求曲線y=f(x)在點(1,f(1))處的切線l的方程;
. (Ⅰ)若a=2,求曲線y=f(x)在點(1,f(1))處的切線l的方程;
(Ⅱ)設函數g(x)=f'(x)有兩個極值點x1 , x2 , 其中x1∈(0,e),求g(x1)﹣g(x2)的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年3月27日,一則“清華大學要求從2017級學生開始,游泳達到一定標準才能畢業”的消息在體育界和教育界引起了巨大反響.游泳作為一項重要的求生技能和運動項目受到很多人的喜愛.其實,已有不少高校將游泳列為必修內容.某中學為了解2017屆高三學生的性別和喜愛游泳是否有關,對100名高三學生進行了問卷調查,得到如下列聯表:
喜歡游泳 | 不喜歡游泳 | 合計 | |
男生 | 10 | ||
女生 | 20 | ||
合計 |
已知在這100人中隨機抽取1人,抽到喜歡游泳的學生的概率為 ![]() .
.
(Ⅰ)請將上述列聯表補充完整;
(Ⅱ)判斷是否有99.9%的把握認為喜歡游泳與性別有關?
附: ![]()
p(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知AD與BC是四面體ABCD中相互垂直的棱,若AD=BC=6,且∠ABD=∠ACD=60°,則四面體ABCD的體積的最大值是( )
A.![]()
B.![]()
C.18
D.36
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com