
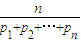 為p1,p2,…,pn的“均倒數(shù)”.已知數(shù)列{an}的各項均為正數(shù),且其前n項的“均倒數(shù)”為
為p1,p2,…,pn的“均倒數(shù)”.已知數(shù)列{an}的各項均為正數(shù),且其前n項的“均倒數(shù)”為 .
. ,試判斷并說明cn+1-cn(n∈N*)的符號;
,試判斷并說明cn+1-cn(n∈N*)的符號;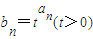 ,記數(shù)列{bn}的前n項和為Sn,試求
,記數(shù)列{bn}的前n項和為Sn,試求 的值;
的值; ,是否存在最大的實數(shù)λ,使當(dāng)x≤λ時,對于一切正整數(shù)n,都有f(x)≤0恒成立?
,是否存在最大的實數(shù)λ,使當(dāng)x≤λ時,對于一切正整數(shù)n,都有f(x)≤0恒成立?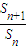 的值;
的值;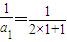 ,解得a1=3=4×1-1,
,解得a1=3=4×1-1,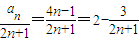 ,cn+1=
,cn+1=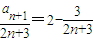 ,
,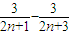 >0,即cn+1>cn.(7分)
>0,即cn+1>cn.(7分)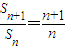 ;(8分)
;(8分)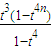 ,
,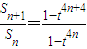 .(10分)
.(10分)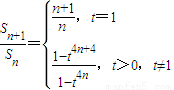 (11分)
(11分)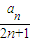 ≤0恒成立,
≤0恒成立,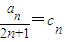 (n∈N+).
(n∈N+).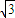 或x≤2-
或x≤2-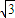 .
.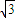 (14分)
(14分)

 名校課堂系列答案
名校課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| 4 |
| y2 |
| 5 |
| P1P2 |
| 3 |
| 4 |
| 3 |
| 2 |
| OP1 |
| OP2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| 4 |
| y2 |
| 5 |
| P1P2 |
| 3 |
| 4 |
| 3 |
| 2 |
| OP1 |
| OP2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| x2 |
| 4 |
| y2 |
| 5 |
| P1P2 |
| 2 |
| 3 |
| op1 |
| OP2 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
(09年湖北鄂州5月模擬理)已知兩定點A(-3,0),B(3,0),動圓M與直線AB相切于點N,且![]() ,現(xiàn)分別過點A、B作動圓M的切線(異于直線AB),兩切線相交于點P.
,現(xiàn)分別過點A、B作動圓M的切線(異于直線AB),兩切線相交于點P.
⑴求動點P的軌跡方程;
⑵若直線xmy3=0截動點P的軌跡所得的弦長為5,求m的值;
⑶設(shè)過軌跡上的點P的直線與兩直線查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2012年四川省南充高中第二次高考適應(yīng)性考試數(shù)學(xué)試卷(理科)(解析版) 題型:解答題
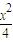 -
-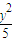 =1(x>2),O是坐標(biāo)原點.
=1(x>2),O是坐標(biāo)原點.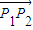 所成的比為λ(λ>0),當(dāng)λ∈[
所成的比為λ(λ>0),當(dāng)λ∈[ ,
, ]時,求|
]時,求|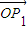 |•|
|•|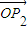 |的最值.
|的最值.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com