
【題目】已知函數f(x)= ![]() 是奇函數
是奇函數
(1)求a的值;
(2)判斷函數的單調性,并給予證明.
【答案】
(1)解:∵f(x)是奇函數,
∴f(﹣x)=﹣f(x)
即 ![]() ,
,
即 ![]()
整理得:(2x﹣1)(a﹣2)=0對任意x∈R都成立,
∴a﹣2=0,
即a=2
(2)解:此時 ![]() ,
,
f(x)在x∈R是增函數,理由如下:
證法一:任取x1,x2∈R,且x1<x2
則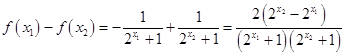
∵x1<x2,且函數y=2x是增函數,
∴ ![]() <0,
<0, ![]() >0
>0
∴f(x1)﹣f(x2)<0,
所以函數f(x)在R是增函數.
證法二:∵ ![]() ,
,
∴ 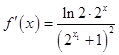 ,
,
∵f′(x)>0恒成立,
所以函數f(x)在R是增函數
【解析】(1)由函數f(x)= ![]() 是奇函數,f(﹣x)=﹣f(x)恒成立,可得a的值;(2)f(x)在x∈R是增函數,
是奇函數,f(﹣x)=﹣f(x)恒成立,可得a的值;(2)f(x)在x∈R是增函數,
證法一:任取x1 , x2∈R,且x1<x2 , 作差判斷出f(x1)﹣f(x2)<0,結合單調性的定義,可得:函數f(x)在R是增函數;
證法二:求導,根據f′(x)>0恒成立,可得:函數f(x)在R是增函數.
【考點精析】認真審題,首先需要了解函數單調性的判斷方法(單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較),還要掌握函數的奇偶性(偶函數的圖象關于y軸對稱;奇函數的圖象關于原點對稱)的相關知識才是答題的關鍵.


科目:高中數學 來源: 題型:
【題目】某醫藥研究所開發一種新藥,如果成年人按規定的劑量服用,據監測,服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線.據進一步測定,每毫升血液中含藥量不少于0.25微克時,治療疾病有效,則服藥一次治療該疾病有效的時間為( ) 
A.4小時
B.![]()
C.![]()
D.5小時
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為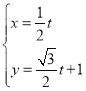 (
(![]() 為參數),曲線
為參數),曲線![]() 的普通方程為
的普通方程為![]() ,以坐標原點為極點,
,以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(I)求直線![]() 的極坐標方程與曲線
的極坐標方程與曲線![]() 的參數方程;
的參數方程;
(II)設點D在曲線![]() 上,且曲線
上,且曲線![]() 在點D處的切線與直線
在點D處的切線與直線![]() 垂直,試確定點D的坐標.
垂直,試確定點D的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() .
.
(Ⅰ)求函數f(x)的定義域;
(Ⅱ)判定f(x)的奇偶性并證明;
(Ⅲ)用函數單調性定義證明:f(x)在(1,+∞)上是增函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數g(x)=3x , h(x)=9x .
(1)解方程:h(x)﹣8g(x)﹣h(1)=0;
(2)令p(x)= ![]() ,求值:p(
,求值:p( ![]() )+p(
)+p( ![]() )+…+p(
)+…+p( ![]() )+p(
)+p( ![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,分別根據下列條件解三角形,其中有兩個解的是( )
A.a=7,b=14,A=30°
B.a=20,b=26,A=150°
C.a=30,b=40,A=30°
D.a=72,b=60,A=135°
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】原命題:“![]() ,
,![]() 為兩個實數,若
為兩個實數,若![]() ,則
,則![]() ,
,![]() 中至少有一個不小于1”,下列說法錯誤的是
中至少有一個不小于1”,下列說法錯誤的是
A.逆命題為:若![]() ,
,![]() 中至少有一個不小于1則
中至少有一個不小于1則![]() ,為假命題
,為假命題
B.否命題為:若![]() 則
則![]() ,
,![]() 都小于1 ,為假命題
都小于1 ,為假命題
C.逆否命題為:若![]() ,
,![]() 都小于1則
都小于1則![]() ,為真命題
,為真命題
D.“![]() ”是“
”是“![]() ,
,![]() 中至少有一個不小于1”的必要不充分條件
中至少有一個不小于1”的必要不充分條件
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對于任意實數x,不等式ax2+2ax﹣(a+2)<0恒成立,則實數a的取值范圍是( )
A.﹣1≤a≤0
B.﹣1≤a<0
C.﹣1<a≤0
D.﹣1<a<0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新生兒Apgar評分,即阿氏評分是對新生兒出生后總體狀況的一個評估,主要從呼吸、心率、反射、膚色、肌張力這幾個方面評分,滿10分者為正常新生兒,評分7分以下的新生兒考慮患有輕度窒息,評分在4分以下考慮患有重度窒息,大部分新生兒的評分多在7-10分之間,某市級醫院婦產科對1月份出生的新生兒隨機抽取了16名,以下表格記錄了他們的評分情況.
(1)現從16名新生兒中隨機抽取3名,求至多有1名評分不低于9分的概率;
(2)以這16名新生兒數據來估計本年度的總體數據,若從本市本年度新生兒任選3名,記![]() 表示抽到評分不低于9分的新生兒數,求
表示抽到評分不低于9分的新生兒數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com