【題目】已知函數f（x）=|x﹣a|+2|x+b|（a＞0，b＞0）的最小值為1．
（1）求a+b的值；
（2）若 
恒成立，求實數m的最大值．
【答案】
（1）解：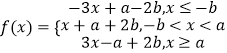 
f（x）在區間（﹣∞，﹣b]上遞減，在區間[﹣b，+∞）上遞增，
所以f（x）min=a+b．
所以a+b=1．
（2）解：因為a＞0，b＞0，且a+b=1，
所以 
，
又因為 
，當且僅當 
時，等號成立，
所以 
時， 
有最小值 
．
所以 
，所以實數m的最大值為
【解析】（1）寫出分段函數，得出f（x）min=a+b，即可求a+b的值；（2）因為a＞0，b＞0，且a+b=1，利用“1”的代換，求最值，根據 
恒成立，求實數m的最大值．
【考點精析】關于本題考查的絕對值不等式的解法，需要了解含絕對值不等式的解法：定義法、平方法、同解變形法，其同解定理有；規律：關鍵是去掉絕對值的符號才能得出正確答案．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】若對任意的正整數
，總存在正整數
，使得數列
的前項和
，則稱是“回歸數列”.
（1）①前項和為
的數列是否是“回歸數列”?并請說明理由；
②通項公式為
的數列
是否是“回歸數列”?并請說明理由；
（2）設是等差數列，首項
，公差
，若是“回歸數列”，求
的值；
（3）是否對任意的等差數列，總存在兩個“回歸數列”和
，使得
成立，請給出你的結論，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四邊形
是正方形，
與
均是以
為直角頂點的等腰直角三角形，點
是
的中點，點
是邊
上的任意一點.
（1）求證：
：
（2）在平面
中，是否總存在與平面
平行的直線？若存在，請作出圖形并說明：若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點F（1，0），點A是直線l1：x=﹣1上的動點，過A作直線l2 ， l1⊥l2 ， 線段AF的垂直平分線與l2交于點P．
（Ⅰ）求點P的軌跡C的方程；
（Ⅱ）若點M，N是直線l1上兩個不同的點，且△PMN的內切圓方程為x2+y2=1，直線PF的斜率為k，求 
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=ln（2ax+1）+ 
﹣x2﹣2ax（a∈R）．
（1）若x=2為f（x）的極值點，求實數a的值；
（2）若y=f（x）在[3，+∞）上為增函數，求實數a的取值范圍；
（3）當a=﹣ 
時，方程f（1﹣x）= 
有實根，求實數b的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在三棱柱ABC﹣A1B1C1中，已知側面ABB1A1是菱形，側面BCC1B1是正方形，點A1在底面ABC的投影為AB的中點D．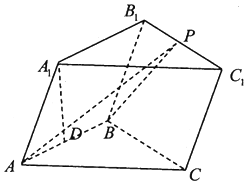 
（1）證明：平面AA1B1B⊥平面BB1C1C；
（2）設P為B1C1上一點，且 
，求二面角A1﹣AB﹣P的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的公差d不為0，且 
， 
，…， 
，…（k1＜k2＜…＜kn＜…）成等比數列，公比為q．
（1）若k1=1，k2=3，k3=8，求 
的值；
（2）當 為何值時，數列{kn}為等比數列；
（3）若數列{kn}為等比數列，且對于任意n∈N* ， 不等式 
恒成立，求a1的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
