Question

設E，F是正方體AC₁的棱AB和D₁C₁的中點，在正方體的12條面對角線中，與截面A₁ECF成60°角的對角線的數目是(　　)

A．0

B．2

C．4

D．6

Answer 1

C

解析考點：直線與平面所成的角．
分析：先把六個面分為三組，在一組組的進行研究，找到直線與截面法向量的夾角即可得到結論．

解：首先，把六個面分成三組，AA₁D₁D和BB₁C₁C對截面的關系是一樣的，其他四個是一樣的，
以點D為原點，AD所在直線為X軸，DC所在直線為Y軸，DD₁所在直線為Z軸，
設正方體棱長為2；
則A（2，0，0），D（0，0，0），B（2，2，0），C（0，2，0），E（2，1，0），
F（0，1，2），A₁（2，0，2），B₁（2，2，2，），C₁（0，2，2），D₁（0，0，2）；
∴=（-2，1，0），=（（0，1，2），=（-2，2，0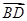），=（-2，-2，0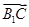），=（-2，0，-2），=（0，-2，-2）；=（0，2，-2）
因為要想面對角線截面A₁ECF成60°角，需要直線與法向量的夾角為30度，即其余弦值為±．
設截面A₁ECF的法向量為=（x，y，z），
由??=（1，2，1），且||=，
因為cos＜，＞===≠±；
cos＜，＞==-，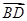
cos＜，＞=≠±；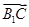
cos（，＞==-；
cos＜，＞=≠±；
再看AA₁D₁D這個面里，
AD₁與EF平行，不是，
所以，一共四條．
故選：C．