（本題滿分14分）從裝有2只紅球,2只白球和1只黑球的袋中逐一取球,已知每只球被抽取的可能性相同．
（Ⅰ）若抽取后又放回,抽取3次,求恰好抽到2次為紅球的概率;
（Ⅱ）若抽取后不放回,設抽完紅球所需的次數為
,求的分布列及期望．
科目：高中數學 來源： 題型：解答題
某中學在高三開設了4門選修課，每個學生必須且只需選修1門選修課。對于該年級的甲、乙、丙3名學生，回答下面的問題：
（1）求這3名學生選擇的選修課互不相同的概率；
（2）某一選修課被這3名學生選修的人數的數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
甲、乙兩名籃球運動員互不影響地在同一位置投球，命中率分別為
與
，且乙投球2次均未命中的概率為
。
（1）求乙投球的命中率。
（2）若甲投球1次，乙投球2次，兩人共命中的次數記為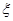
，求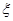的分布列和數學期望。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）某項選拔共有四輪考核，每輪設有一個問題，能正確回答問題者進入下一輪考核，否則即被淘汰．已知某選手能正確回答第一、二、三、四輪的問題的概率分別為
、
、
、
，且各輪問題能否正確回答互不影響．
（1）求該選手進入第四輪才被淘汰的概率;
（2）求該選手至多進入第三輪考核的概率． （注：本小題結果可用分數表示）
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
（本小題滿分12分）在一個選拔項目中，每個選手都需要進行4輪考核，每輪設有一個問題，能正確回答者進入下一輪考核，否則被淘汰。已知某選手能正確回答第一、二、三、四輪問題的概率分別為
、
、
、
，且各輪問題能否正確回答互不影響。
（Ⅰ）求該選手進入第三輪才被淘汰的概率；
（Ⅱ）求該選手至多進入第三輪考核的概率；
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
中華人民共和國《道路交通安全法》中將飲酒后違法駕駛機動車的行為分成兩個檔次：“酒后駕車”和“醉酒駕車”，其檢測標準是駕駛人員血液中的酒精含量Q（簡稱血酒含量，單位是毫克/100毫升），當20≤Q≤80時，為酒后駕車；當Q＞80時，為醉酒駕車.濟南市公安局交通管理部門于2011年2月的某天晚上8點至11點在市區設點進行一次攔查行動，共依法查出了60名飲酒后違法駕駛機動車者，如圖為這60名駕駛員抽血檢測后所得結果畫出的頻率分布直方圖（其中Q≥140的人數計入120≤Q＜140人數之內）.
（1） 求此次攔查中醉酒駕車的人數；
（2） 從違法駕車的60人中按酒后駕車和醉酒駕車利用分層抽樣抽取8人做樣本進行研究，
再從抽取的8人中任取3人，求3人中含有醉酒駕車人數x的分布列和期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
--------------------------------2分 
-----------4分
-----------------------------------------------------1分
,
,
,
．----------------------------------------------4分 
．--------------------------3分
