
【題目】已知![]() ,
,![]() .
.
(1)討論![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)當(dāng)![]() 時(shí),證明:
時(shí),證明:![]() .
.
【答案】(1)![]() 在
在![]() 上單調(diào)遞減;在
上單調(diào)遞減;在![]() 和
和![]() 上單調(diào)遞增.(2)見解析
上單調(diào)遞增.(2)見解析
【解析】
(1)先求函數(shù)的定義域,再進(jìn)行求導(dǎo)得![]() ,對
,對![]() 分成
分成![]() ,
,![]() ,
,![]() 三種情況討論,求得單調(diào)區(qū)間;
三種情況討論,求得單調(diào)區(qū)間;
(2)要證由![]() ,等價(jià)于證明
,等價(jià)于證明![]() ,再對
,再對![]() 分
分![]() ,
,![]() 兩種情況討論;證明當(dāng)
兩種情況討論;證明當(dāng)![]() 時(shí),不等式成立,可先利用放縮法將參數(shù)
時(shí),不等式成立,可先利用放縮法將參數(shù)![]() 消去,轉(zhuǎn)化成證明不等式
消去,轉(zhuǎn)化成證明不等式![]() 成立,再利用構(gòu)造函數(shù)
成立,再利用構(gòu)造函數(shù)![]() ,利用導(dǎo)數(shù)證明其最小值大于0即可。
,利用導(dǎo)數(shù)證明其最小值大于0即可。
(1)![]() 的定義域?yàn)?/span>
的定義域?yàn)?/span>![]() ,
,
![]() ,
,
當(dāng)![]() 時(shí),由
時(shí),由![]() ,得
,得![]() ;
;
由![]() ,得
,得![]() ,
,
所以![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),由
時(shí),由![]() ,得
,得![]() 或
或![]() ;
;
由![]() ,得
,得![]() ;
;
所以![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 和
和![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),由
時(shí),由![]() ,得
,得![]() 在
在![]() 上單調(diào)遞增;
上單調(diào)遞增;
當(dāng)![]() 時(shí),由
時(shí),由![]() ,得
,得![]() 或
或![]() ;由
;由![]() ,得
,得![]() ;
;
所以![]() 在
在![]() 上單調(diào)遞減;在
上單調(diào)遞減;在![]() 和
和![]() 上單調(diào)遞增.
上單調(diào)遞增.
(2)由![]() ,得
,得![]() ,
,
①當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() ,不等式顯然成立;
,不等式顯然成立;
②當(dāng)![]() 時(shí),
時(shí),![]() ,由
,由![]() ,得
,得![]() ,
,
所以只需證:![]() ,
,
即證![]() ,令
,令![]() ,
,
則![]() ,
,![]() ,
,
令![]() ,
,
則![]() ,
,
令![]() ,
,
則![]() ,
,
所以![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
因?yàn)?/span>![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,
,
所以![]() 在
在![]() 上單調(diào)遞減,在
上單調(diào)遞減,在![]() 上單調(diào)遞增,
上單調(diào)遞增,
又因?yàn)?/span>![]() ,
,![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
當(dāng)![]() 時(shí),
時(shí),![]() ,
,![]() 在
在![]() 上單調(diào)遞增,
上單調(diào)遞增,
所以![]() ,
,
所以![]() ,
,
所以原命題得證


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() 的中點(diǎn)為
的中點(diǎn)為![]() .
.
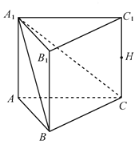
(Ⅰ)求證:![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)在棱![]() 上是否存在點(diǎn)
上是否存在點(diǎn)![]() ,使得
,使得![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】黃岡“一票通”景區(qū)旅游年卡,是由黃岡市旅游局策劃,黃岡市大別山旅游公司推出的一項(xiàng)惠民工程,持有旅游年卡一年內(nèi)可不限次暢游全市19家簽約景區(qū).為了解市民每年旅游消費(fèi)支出情況![]() 單位:百元
單位:百元![]() ,相關(guān)部門對已游覽某簽約景區(qū)的游客進(jìn)行隨機(jī)問卷調(diào)查,并把得到的數(shù)據(jù)列成如表所示的頻數(shù)分布表:
,相關(guān)部門對已游覽某簽約景區(qū)的游客進(jìn)行隨機(jī)問卷調(diào)查,并把得到的數(shù)據(jù)列成如表所示的頻數(shù)分布表:
組別 |
|
|
|
|
|
頻數(shù) | 10 | 390 | 400 | 188 | 12 |
![]() 求所得樣本的中位數(shù)
求所得樣本的中位數(shù)![]() 精確到百元
精確到百元![]() ;
;
![]() 根據(jù)樣本數(shù)據(jù),可近似地認(rèn)為市民的旅游費(fèi)用支出服從正態(tài)分布
根據(jù)樣本數(shù)據(jù),可近似地認(rèn)為市民的旅游費(fèi)用支出服從正態(tài)分布![]() ,若該市總?cè)丝跒?/span>750萬人,試估計(jì)有多少市民每年旅游費(fèi)用支出在7500元以上;
,若該市總?cè)丝跒?/span>750萬人,試估計(jì)有多少市民每年旅游費(fèi)用支出在7500元以上;
![]() 若年旅游消費(fèi)支出在
若年旅游消費(fèi)支出在![]() 百元
百元![]() 以上的游客一年內(nèi)會(huì)繼續(xù)來該景點(diǎn)游玩現(xiàn)從游客中隨機(jī)抽取3人,一年內(nèi)繼續(xù)來該景點(diǎn)游玩記2分,不來該景點(diǎn)游玩記1分,將上述調(diào)查所得的頻率視為概率,且游客之間的選擇意愿相互獨(dú)立,記總得分為隨機(jī)變量X,求X的分布列與數(shù)學(xué)期望.
以上的游客一年內(nèi)會(huì)繼續(xù)來該景點(diǎn)游玩現(xiàn)從游客中隨機(jī)抽取3人,一年內(nèi)繼續(xù)來該景點(diǎn)游玩記2分,不來該景點(diǎn)游玩記1分,將上述調(diào)查所得的頻率視為概率,且游客之間的選擇意愿相互獨(dú)立,記總得分為隨機(jī)變量X,求X的分布列與數(shù)學(xué)期望.
![]() 參考數(shù)據(jù):
參考數(shù)據(jù):,
![]() ;
;![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知拋物線![]() ,
,![]() 為其焦點(diǎn),
為其焦點(diǎn),![]() 為其準(zhǔn)線,過
為其準(zhǔn)線,過![]() 任作一條直線交拋物線于
任作一條直線交拋物線于![]() 兩點(diǎn),
兩點(diǎn),![]() 、
、![]() 分別為
分別為![]() 、
、![]() 在
在![]() 上的射影,
上的射影,![]() 為
為![]() 的中點(diǎn),給出下列命題:
的中點(diǎn),給出下列命題:
(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
(4)![]() 與
與![]() 的交點(diǎn)的
的交點(diǎn)的![]() 軸上;(5)
軸上;(5)![]() 與
與![]() 交于原點(diǎn).
交于原點(diǎn).
其中真命題的序號(hào)為_________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于函數(shù)![]() ,若存在正常數(shù)
,若存在正常數(shù)![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]() 成立,我們稱函數(shù)
成立,我們稱函數(shù)![]() 為“
為“![]() 同比不減函數(shù)”.
同比不減函數(shù)”.
(1)求證:對任意正常數(shù)![]() ,
,![]() 都不是“
都不是“![]() 同比不減函數(shù)”;
同比不減函數(shù)”;
(2)若函數(shù)![]() 是“
是“![]() 同比不減函數(shù)”,求
同比不減函數(shù)”,求![]() 的取值范圍;
的取值范圍;
(3)是否存在正常數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 為“
為“![]() 同比不減函數(shù)”,若存在,求
同比不減函數(shù)”,若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 為信號(hào)源點(diǎn),
為信號(hào)源點(diǎn),![]() 、
、![]() 、
、![]() 是三個(gè)居民區(qū),已知
是三個(gè)居民區(qū),已知![]() 、
、![]() 都在
都在![]() 的正東方向上,
的正東方向上,![]() ,
,![]() ,
,![]() 在
在![]() 的北偏西45°方向上,
的北偏西45°方向上,![]() ,現(xiàn)要經(jīng)過點(diǎn)
,現(xiàn)要經(jīng)過點(diǎn)![]() 鋪設(shè)一條總光纜直線
鋪設(shè)一條總光纜直線![]() (
(![]() 在直線
在直線![]() 的上方),并從
的上方),并從![]() 、
、![]() 、
、![]() 分別鋪設(shè)三條最短分支光纜連接到總光纜
分別鋪設(shè)三條最短分支光纜連接到總光纜![]() ,假設(shè)鋪設(shè)每條分支光纜的費(fèi)用與其長度的平方成正比,比例系數(shù)為1元/
,假設(shè)鋪設(shè)每條分支光纜的費(fèi)用與其長度的平方成正比,比例系數(shù)為1元/![]() ,設(shè)
,設(shè)![]() ,(
,(![]() ),鋪設(shè)三條分支光纜的總費(fèi)用為
),鋪設(shè)三條分支光纜的總費(fèi)用為![]() (元).
(元).
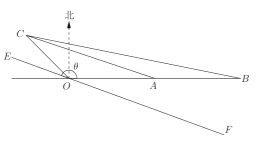
(1)求![]() 關(guān)于
關(guān)于![]() 的函數(shù)表達(dá)式;
的函數(shù)表達(dá)式;
(2)求![]() 的最小值及此時(shí)
的最小值及此時(shí)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,三棱錐D-ABC中,![]()
![]()
![]() ,E,F分別為DB,AB的中點(diǎn),且
,E,F分別為DB,AB的中點(diǎn),且![]() .
.
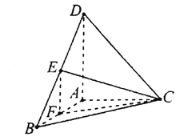
(1)求證:平面![]() 平面ABC;
平面ABC;
(2)求二面角D-CE-F的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 是由兩個(gè)全等的菱形
是由兩個(gè)全等的菱形![]() 和
和![]() 組成的空間圖形,
組成的空間圖形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
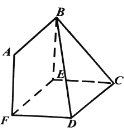
(1)求證:![]() ;
;
(2)如果二面角B-EF-D的平面角為60°,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,過左焦點(diǎn)
,過左焦點(diǎn)![]() 的直線與橢圓交于
的直線與橢圓交于![]() ,
,![]() 兩點(diǎn),且線段
兩點(diǎn),且線段![]() 的中點(diǎn)為
的中點(diǎn)為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設(shè)![]() 為
為![]() 上一個(gè)動(dòng)點(diǎn),過點(diǎn)
上一個(gè)動(dòng)點(diǎn),過點(diǎn)![]() 與橢圓
與橢圓![]() 只有一個(gè)公共點(diǎn)的直線為
只有一個(gè)公共點(diǎn)的直線為![]() ,過點(diǎn)
,過點(diǎn)![]() 與
與![]() 垂直的直線為
垂直的直線為![]() ,求證:
,求證:![]() 與
與![]() 的交點(diǎn)在定直線上,并求出該定直線的方程.
的交點(diǎn)在定直線上,并求出該定直線的方程.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com