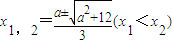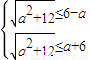已知a為實數,f(x)=(x2-4)(x-a).
(1)求導數f′(x).
(2)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值.
(3)若f(x)在(-∞,-2)和[2,+∞]上都是遞增的,求a的取值范圍.
【答案】
分析:(1)按導數的求導法則求解
(2)由f′(-1)=0代入可得f(x),先求導數,研究函數的極值點,通過比較極值點與端點的大小從而確定出最值
(3)(法一)由題意可得f′(2)≥0,f′(-2)≥0聯立可得a的范圍
(法二)求出f′(x),再求單調區增間(-∞,x
1)和[x
2,+∞),依題意有(-∞,-2)⊆(-∞,x
1)[2,+∞]⊆[x
2,+∞)
解答:解:(1)由原式得f(x)=x
3-ax
2-4x+4a,∴f'(x)=3x
2-2ax-4.
(2)由f'(-1)=0得
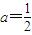
,此時有
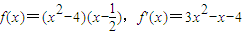
.
由f'(x)=0得
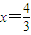
或x=-1,又
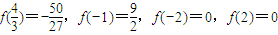
,
所以f(x)在[-2,2]上的最大值為

,最小值為
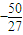
.
(3)解法一:f'(x)=3x
2-2ax-4的圖象為開口向上且過點(0,-4)的拋物線,由條件得f'(-2)≥0,f'(2)≥0,
∴-2≤a≤2.
所以a的取值范圍為[-2,2].
解法二:令f'(x)=0即3x
2-2ax-4=0,由求根公式得:
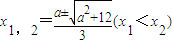
所以f'(x)=3x
2-2ax-4.在(-∞,x
1]和[x
2,+∞)上非負.
由題意可知,當x≤-2或x≥2時,f'(x)≥0,
從而x
1≥-2,x
2≤2,
即
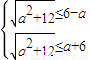
解不等式組得-2≤a≤2.
∴a的取值范圍是[-2,2].
點評:本題考查了導數的求解,利用導數求閉區間上函數的最值,求函數在閉區間[a,b]上的最大值與最小值是通過比較函數在
(a,b)內所有極值與端點函數f(a),f(b) 比較而得到的.利用導數求單調區間要區分“單調區間”和“在區間上單調遞增”兩個不同概念.

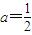 ,此時有
,此時有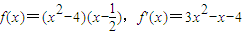 .
.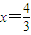 或x=-1,又
或x=-1,又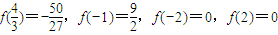 ,
, ,最小值為
,最小值為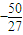 .
.