【題目】下面給出的命題中：
（1）已知函數
，則
；
（2）“
”是“直線
與直線
互相垂直”的必要不充分條件；
（3）已知隨機變量
服從正態分布
，且
，則
；
（4）已知圓
，圓
，則這兩個圓恰有兩條公切線.
其中真命題的個數為
A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】(1)由
=sina,可得
=sin
=1,故(1)正確；
(2)直線(m+2)x+my+1=0與直線(m2)x+(m+2)y3=0互相垂直(m+2)(m2)+m(m+2)=0，
即m=2或m=1.
∴“m=2”是“直線(m+2)x+my+1=0與直線(m2)x+(m+2)y3=0互相垂直”的充分不必要條件,故(2)錯誤；
(3)隨機變量ξ服從正態分布
,且P(2ξ0)=0.4,則P(ξ>2)=0.1,故(3)錯誤；
(4)圓
化為(x+1)2+y2=1,圓
化為
=1，兩圓的圓心距d=1，小于兩半徑之和，兩圓相交，∴這兩個圓恰有兩條公切線,故(4)正確。
∴正確的命題是2個。
故選：B.
科目：高中數學 來源： 題型：
【題目】設函數f(x)的定義域為(－3,3)，
滿足f(－x)＝－f(x)，且對任意x，y，都有f(x)－f(y)＝f(x－y)，當x<0時，f(x)>0，f(1)＝－2.
(1)求f(2)的值；
(2)判斷f(x)的單調性，并證明；
(3)若函數g(x)＝f(x－1)＋f(3－2x)，求不等式g(x)≤0的解集．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，∠BAC=90°，AB=AC=2，AA1=6，點E、F分別在棱BB1、CC1上，且BE= 
BB1 ， C1F= CC1 ． 
（1）求平面AEF與平面ABC所成角α的余弦值；
（2）若G為BC的中點，A1G與平面AEF交于H，且設 
= 
，求λ的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設數列{an}的前n項和是Sn ， 若點An（n， 
）在函數f（x）=﹣x+c的圖象上運動，其中c是與x無關的常數，且a1=3（n∈N*）．
（1）求數列{an}的通項公式；
（2）記bn=a 
，求數列{bn}的前n項和Tn的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】菜農定期使用低害殺蟲農藥對蔬菜進行噴灑，以防止害蟲的危害，但采集上市時蔬菜仍存有少量的殘留農藥，食用時需要用清水清洗干凈，下表是用清水
(單位：千克)清洗該蔬菜
千克后，蔬菜上殘留的農藥
(單位：微克)的統計表：
在坐標系中描出散點圖，并判斷變量
與
的相關性；
（2）若用解析式
作為蔬菜農藥殘量
與用水量
的回歸方程，令
，計算平均值
和
，完成以下表格(填在答題卡中)，求出
與
的回歸方程．(
精確到0.1)
（3）對于某種殘留在蔬菜上的農藥，當它的殘留量低于20微克時對人體無害，為了放心食用該蔬菜，請估計需要用多少千克的清水清洗一千克蔬菜？(精確到0.1，參考數據
)（附：線性回歸方程計算公式： 
， 
）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某投資人欲將5百萬元獎金投入甲、乙兩種理財產品，根據銀行預測，甲、乙兩種理財產品的收益與投入獎金
的關系式分別為
，其中
為常數且
.設對乙種產品投入獎金
百萬元，其中
．
（1）當
時，如何進行投資才能使得總收益
最大；（總收益
）
（2）銀行為了吸儲，考慮到投資人的收益，無論投資人獎金如何分配，要使得總收益不低于
，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】公差不為0的等差數列
中，已知
且
，其前
項和
的最大值為（ ）
A. 25 B. 26 C. 27 D. 28
【答案】B
【解析】設等差數列
的公差為
,
∵
，
∴
，
整理得
，
∵
，
∴
．
∴
，
∴當
時， 
．
故
最大，且
．選B．
點睛：求等差數列前n項和最值的常用方法：
①利用等差數列的單調性， 求出其正負轉折項，便可求得和的最值；
②將等差數列的前n項和
(A、B為常數)看作關于n的二次函數，根據二次函數的性質求最值．
【題型】單選題
【結束】
9
【題目】如圖，網格紙上小正方形的邊長為1，粗實線畫出的是某多面體的三視圖，則該多面體的表面積為（ ）
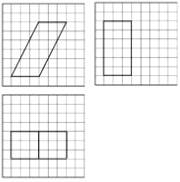
A. 
B. 
C. 90 D. 81
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
