
定義域為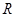 的函數
的函數 ,若函數
,若函數 有
有 個不同的零點
個不同的零點 ,
, ,
, ,
, ,
, ,則
,則 等于_______________
等于_______________
15
解析試題分析:根據已知條件可知,分段函數f(x)的圖像,再單獨定義一個(1,1)點即可。
整個函數圖像是關于x=1對稱的,且f(x)>0恒成立。函數 有
有 個不同的零點
個不同的零點 ,
, ,
, ,
, ,
, ,不妨令
,不妨令








因為從總體上來說f(x)是一個關于f(x)的二次函數,即最多只會有2個不同的f(x)解,那么只能是每個f(x)對應了2個不等的與x=1對稱的關于x的實根,再加上x=1,一共就有5個了!所以說
因為f(1)=1,則 ,代入點(1,0)到
,代入點(1,0)到 中,有1+b+
中,有1+b+ =0,b=-
=0,b=-
所以f(x)=0,則有 ,當f(x)=1時則有
,當f(x)=1時則有
當f(x)= 時則有
時則有 ,因此可知
,因此可知 =15,故答案為15.
=15,故答案為15.
考點:本試題考查了函數與方程的運用。
點評:解決該試題的關鍵是理解方程的根與函數f(x)的關系,然后結合分段函數的圖像來得到各個交點具有的對稱性,進而得到運算的結果,屬于難度題。


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:高中數學 來源: 題型:填空題
函數 ,其中
,其中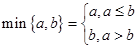 ,若動直線
,若動直線 與函數
與函數 的圖像有三個不同的交點,它們的橫坐標分別為
的圖像有三個不同的交點,它們的橫坐標分別為 ,則
,則 是否存在最大值?若存在,在橫線處填寫其最大值;若不存在,直接填寫“不存在”_______________.
是否存在最大值?若存在,在橫線處填寫其最大值;若不存在,直接填寫“不存在”_______________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com