選修4-5:不等式選講
設函數f(x)=|x-a|+3x,其中a>0.
(Ⅰ)當a=1時,求不等式f(x)≥3x+2的解集
(Ⅱ)若不等式f(x)≤0的解集為{x|x≤-1},求a的值.
【答案】
分析:(Ⅰ)當a=1時,f(x)≥3x+2可化為|x-1|≥2.直接求出不等式f(x)≥3x+2的解集即可.
(Ⅱ)由f(x)≤0得|x-a|+3x≤0分x≥a和x≤a推出等價不等式組,分別求解,然后求出a的值.
解答:解:(Ⅰ)當a=1時,f(x)≥3x+2可化為
|x-1|≥2.
由此可得x≥3或x≤-1.
故不等式f(x)≥3x+2的解集為
{x|x≥3或x≤-1}.
(Ⅱ)由f(x)≤0得
|x-a|+3x≤0
此不等式化為不等式組
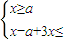
或

即

或
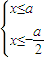
因為a>0,所以不等式組的解集為{x|x

}
由題設可得-

=-1,故a=2
點評:本題是中檔題,考查絕對值不等式的解法,注意分類討論思想的應用,考查計算能力,常考題型.

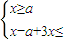 或
或
 或
或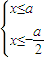
 }
} =-1,故a=2
=-1,故a=2

 百年學典課時學練測系列答案
百年學典課時學練測系列答案 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案