【題目】設函數f(x)＝loga(1＋
x)，g(x)＝loga(1－x)，(a>0且a≠1)，若h(x)＝f(x)－g(x)．
(1)求函數h(x)的定義域；
(2)判斷h(x)的奇偶性，并說明理由；
(3)若f(2)＝1，求使h(x)>0成立的x的集合．
【答案】(1)（-2,2）
(2) h(x)為奇函數
(3) 
【解析】
（1）根據函數定義域的定義，列出使得
有意義的條件，即可求解函數的定義域；
（2）根據函數的奇偶性性的定義，即可作出證明，得到函數的奇偶性；
（3）由
，求得
，得到函數的解析式，再由
，得到不等式
，即可求得不等式的解集.
(1)由1+
x>0且1-
x>0得-2<x<2,所以函數定義域為（-2,2）
(2)∵對任意的x∈(－2,2)，－x∈(－2,2)，
所以h(x)為奇函數
(3) f(2)＝1，得a＝2.此時h(x)＝log2(1＋x)－log2(1－x)，
由h(x)>0得:1＋x>1－x，所以x>0
又由（1）知 -2<x<2所以0<x<2，
x的取值集合為
第1卷單元月考期中期末系列答案科目：高中數學 來源： 題型：
【題目】（選修4﹣4：坐標系與參數方程）
已知曲線C1的參數方程為 
（t為參數），以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ=2sinθ．
（1）把C1的參數方程化為極坐標方程；
（2）求C1與C2交點的極坐標（ρ≥0，0≤θ＜2π）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
在點
處的切線方程為
.
（1）求函數
的解析式；
（2）求函數
的單調區間和極值.
【答案】（1）
;（2）見解析.
【解析】試題分析：（1）根據導數幾何意義得
，再與
聯立方程組解得
， 
（2）先函數導數,再求導函數零點,列表分析導函數符號變化規律,進而確定單調區間和極值
試題解析：（1）
，切線為
，即斜率
，縱坐標
即
， 
，解得
， 
解析式
（2）
，定義域為
得到
在
單增，在
單減，在
單增
極大值
，極小值
.
【題型】解答題
【結束】
20
【題目】如圖：在四棱錐
中，底面
為菱形，且
， 
底面
，
， 
， 
是
上點，且
平面
.
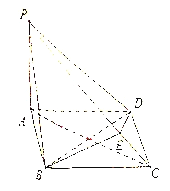
（1）求證： 
；（2）求三棱錐
的體積.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在框圖中，設x=2，并在輸入框中輸入n=4；ai=i（i=0，1，2，3，4）．則此程序執行后輸出的S值為（ ） 
A.26
B.49
C.52
D.98
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知命題
：若關于
的方程
無實數根，則
；命題
：若關于
的方程
有兩個不相等的正實數根，則
.
(1)寫出命題
的否命題，并判斷命題
的真假；
(2)判斷命題“
且
”的真假，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
： 
的兩個焦點分別為
， 
，且點
在橢圓
上.
（1）求橢圓
的標準方程；
（2）設橢圓
的左頂點為
，過點
的直線
與橢圓
相交于異于
的不同兩點
，求
的面積
的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某高校在
年的自主招生考試成績中隨機抽取
名學生的筆試成績，按成績分組：第
組
，第
組
，第
組
，第
組
，第
組
得到的頻率分布直方圖如圖所示.
（1）分別求第
， 
， 
組的頻率；
（2）若該校決定在筆試成績高的第
， 
， 
組中用分層抽樣抽取
名學生進入第二輪面試，求第
， 
， 
組每組各抽取多少名學生進入第二輪面試？
（3）在（2）的前提下，學校決定在這
名學生中隨機抽取
名學生接受甲考官的面試，求第
組至少有一名學生被甲考官面試的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解籃球愛好者小李的投籃命中率與打籃球時間之間的關系,下表記錄了小李某月1號到5號每天打籃球時間x(單位:小時)與當天投籃命中率y之間的關系:
時間x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李這5天的平均投籃命中率為 ;用線性回歸分析的方法,預測小李該月6號打6小時籃球的投籃命中率為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
