
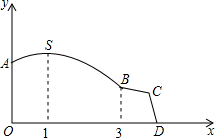
 安通駕校擬圍著一座山修建一條環形訓練道路OASBCD,道路的平面圖如圖所示(單位:km),已知曲線ASB為函數y=Asin(ωx+φ)(A>0,0<ω<1,|φ|<
安通駕校擬圍著一座山修建一條環形訓練道路OASBCD,道路的平面圖如圖所示(單位:km),已知曲線ASB為函數y=Asin(ωx+φ)(A>0,0<ω<1,|φ|<| π |
| 2 |
| 3 |
| 3 |
| ||
| 2 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 12+(4-3)2 |
| 2 |
| BD |
| sin120° |
| CD |
| sinθ |
| BC |
| sin(60°-θ) |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
2
| ||
| 3 |
| π |
| 3 |
| π |
| 6 |
2
| ||
| 3 |


 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com