
【題目】二手車經銷商小王對其所經營的![]() 型號二手汽車的使用年數
型號二手汽車的使用年數![]() 與銷售價格
與銷售價格![]() (單位:萬元/輛)進行整理,得到如下數據:
(單位:萬元/輛)進行整理,得到如下數據:
使用年數 | 2 | 3 | 4 | 5 | 6 | 7 |
售價 | 20 | 12 | 8 | 6.4 | 4.4 | 3 |
| 3.00 | 2.48 | 2.08 | 1.86 | 1.48 | 1.10 |
下面是![]() 關于
關于![]() 的散點圖:
的散點圖:

(I)由散點圖看出,可以用線性回歸模型擬合![]() 和
和![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(II)求![]() 關于
關于![]() 的回歸方程,并預測某輛
的回歸方程,并預測某輛![]() 型號二手汽車當使用年數為9年時,售價大約為多少?(
型號二手汽車當使用年數為9年時,售價大約為多少?(![]() 、
、![]() 的值精確到
的值精確到![]() )
)
(III)基于成本的考慮,該型號二手汽車的售價不得低于7118元,請根據(II)求出的回歸方程預測在收購該型號二手汽車時,車輛的使用年數不得超過多少年?
參考公式: ,相關系數
,相關系數 .
.
參考數據:![]() ,
, ,
, ,
, ,
,![]() ,
,![]() .
.
【答案】見解析
【解析】(I)由表中數據可知,![]() ,
,![]() ,
, ![]() ,由相關系數公式可知
,由相關系數公式可知![]() 和
和![]() 的相關系數
的相關系數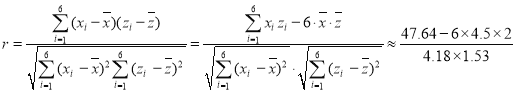
![]() .
.
從而可知![]() 和
和![]() 的線性相關程度很高.………………4分
的線性相關程度很高.………………4分
(II)由(I)及表中數據可知,![]() ,
,![]() ,
,![]() ,
,
則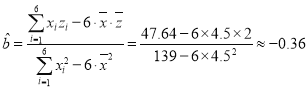 ,
,
![]() ,………………6分
,………………6分
所以![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,即
,即![]() ,即
,即![]() .
.
當![]() 時,
時,![]() ,由參考數據可知
,由參考數據可知![]() (萬元).
(萬元).
由此預測某輛![]() 型號二手汽車當使用年數為9年時,售價大約為1.46萬元.………………8分
型號二手汽車當使用年數為9年時,售價大約為1.46萬元.………………8分
(III)若該型號二手汽車的售價不得低于7118元,即![]() ,
,
則![]() ,即
,即![]() ,(10分)
,(10分)
由(II)可得![]() ,解得
,解得![]() ,
,
所以在收購該型號二手汽車時,車輛的使用年數不得超過11年.………………12分
【命題意圖】本題主要考查散點圖、回歸直線方程,意在考查學生的識圖能力、數據處理能力、運算求解能力.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:
【題目】為響應國家擴大內需的政策,某廠家擬在2016年舉行某一產品的促銷活動,經調查測算,該產品的年銷量(即該廠的年產量)![]() 萬件與年促銷費用
萬件與年促銷費用![]() (
(![]() )萬元滿足
)萬元滿足![]() (
(![]() 為常數).如果不搞促銷活動,則該產品的年銷量只能是1萬件.已知2016年生產該產品的固定投入為6萬元,每生產1萬件該產品需要再投入12萬元,廠家將每件產品的銷售價格定為每件產品平均生產投入成本的1.5倍(生產投入成本包括生產固定投入和生產再投入兩部分).
為常數).如果不搞促銷活動,則該產品的年銷量只能是1萬件.已知2016年生產該產品的固定投入為6萬元,每生產1萬件該產品需要再投入12萬元,廠家將每件產品的銷售價格定為每件產品平均生產投入成本的1.5倍(生產投入成本包括生產固定投入和生產再投入兩部分).
(1)求常數![]() ,并將該廠家2016年該產品的利潤
,并將該廠家2016年該產品的利潤![]() 萬元表示為年促銷費用
萬元表示為年促銷費用![]() 萬元的函數;
萬元的函數;
(2)該廠家2016年的年促銷費用投入多少萬元時,廠家利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() ,向量
,向量![]() 分別為平面直角坐標內
分別為平面直角坐標內![]() 軸正方向上的單位向量,若向量
軸正方向上的單位向量,若向量![]() ,
, ![]() , ,且
, ,且![]() .
.
(Ⅰ)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)設橢圓![]() ,曲線
,曲線![]() 的切線
的切線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,試證:
兩點,試證:![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系中,已知曲線![]() 的參數方程為
的參數方程為 (
(![]() 為參數,
為參數,![]() ).
).
(Ⅰ)當![]() 時,若曲線
時,若曲線![]() 上存在
上存在![]() 兩點關于點
兩點關于點![]() 成中心對稱,求直線
成中心對稱,求直線![]() 的參數方程;
的參數方程;
(Ⅱ)在以原點為極點,![]() 軸的正半軸為極軸的極坐標系中,極坐標方程為
軸的正半軸為極軸的極坐標系中,極坐標方程為![]() 的直線
的直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 兩點,若
兩點,若![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知離心率為![]() 的橢圓
的橢圓![]() :
:![]() 經過點
經過點![]() ,且
,且![]() 是頂點均不與橢圓四個頂點重合的橢圓
是頂點均不與橢圓四個頂點重合的橢圓![]() 一個內接四邊形.
一個內接四邊形.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若![]() ,試判斷
,試判斷![]() 的面積是否為定值?若為定值,求出該定值;若不為定值,請說明理由.
的面積是否為定值?若為定值,求出該定值;若不為定值,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對數列{an}前n項和為Sn , an>0(n=1,2,…),a1=a2=1,且對n≥2有(a1+a2+…+an)an=(a1+a2+…+an﹣1)an+1 , 則S1S2+S2S3+S3S4+…+Sn﹣1Sn= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,
,![]() 為
為![]() 上一點,
上一點,![]() 、
、![]() 為橢圓
為橢圓![]() 的兩焦點,
的兩焦點,![]() 的周長為
的周長為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)設橢圓![]() ,曲線
,曲線![]() 的切線
的切線![]() 交橢圓
交橢圓![]() 于
于![]() 、
、![]() 兩點,試證:
兩點,試證:![]() 的面積為定值.
的面積為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,向量 ![]() =(a+b,sinA﹣sinC),且
=(a+b,sinA﹣sinC),且 ![]() =(c,sinA﹣sinB),且
=(c,sinA﹣sinB),且 ![]() ∥
∥ ![]() .
.
(1)求角B的大小;
(2)若a+c=8,求AC邊上中線長的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,已知a、b、c分別是三內角A、B、C所對應的邊長,且b2+c2﹣a2=bc
(1)求角A的大小;
(2)若sin2A+sin2B=sin2C,試判斷△ABC的形狀并求角B的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com