
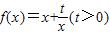 ,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.
,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.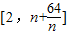 內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值. ,
, 解得x>
解得x> ,或x<-
,或x<- .
. ,
,
 ,∴切線PM的方程為:
,∴切線PM的方程為: .
. .
.
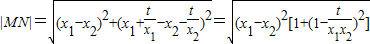

 ,
,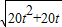 (t>0)
(t>0)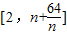 上為增函數,
上為增函數, )對一切的正整數n恒成立
)對一切的正整數n恒成立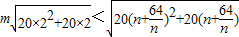 ,
, 對一切的正整數n恒成立
對一切的正整數n恒成立 ,
, .
.


 巧學巧練系列答案
巧學巧練系列答案 課課練江蘇系列答案
課課練江蘇系列答案科目:高中數學 來源:2010-2011學年江蘇省南通市海門中學高二(下)期中數學試卷(理科)(解析版) 題型:解答題
 ,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.
,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.查看答案和解析>>
科目:高中數學 來源:2010-2011學年四川省巴中市通江中學高三(下)4月月考數學試卷(理科)(解析版) 題型:解答題
 ,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.
,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N. 內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.查看答案和解析>>
科目:高中數學 來源:2010年湖北省荊門市龍泉中學高三數學綜合訓練11(理科)(解析版) 題型:解答題
 ,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.
,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N. 內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.查看答案和解析>>
科目:高中數學 來源:2010年江蘇省無錫市江陰市成化高級中學高考數學模擬試卷(01)(解析版) 題型:解答題
 ,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.
,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N. 內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.查看答案和解析>>
科目:高中數學 來源:2010年江蘇省南通市海安中學高考數學模擬試卷(二)(解析版) 題型:解答題
 ,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N.
,過點P(1,0)作曲線y=f(x)的兩條切線PM,PN,切點分別為M,N. 內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.
內,總存在m+1個數a1,a2,…,am,am+1,使得不等式g(a1)+g(a2)+…+g(am)<g(am+1)成立,求m的最大值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com