
【題目】已知函數f(x)=x2﹣4x+a+3,a∈R.
(1)若函數y=f(x)的圖象與x軸無交點,求a的取值范圍;
(2)若函數y=f(x)在[﹣1,1]上存在零點,求a的取值范圍;
(3)設函數g(x)=bx+5﹣2b,b∈R.當a=0時,若對任意的x1∈[1,4],總存在x2∈[1,4],使得f(x1)=g(x2),求b的取值范圍.
【答案】
(1)解:∵函數y=f(x)的圖象與x軸無交點,
∴方程f(x)=0的判別式△<0,
∴16﹣4(a+3)<0,解得a>1,
∴a的取值范圍為(1,+∞);
(2)解:∵f(x)=x2﹣4x+a+3的對稱軸是x=2,
∴y=f(x)在[﹣1,1]上是減函數,
∵y=f(x)在[﹣1,1]上存在零點,
∴必有: ![]() ,即
,即 ![]() ,
,
解得:﹣8≤a≤0,
故實數a的取值范圍為﹣8≤a≤0;
(3)解:若對任意的x1∈[1,4],總存在x2∈[1,4],使f(x1)=g(x2),
只需函數y=f(x)的值域為函數y=g(x)值域的子集.
當a=0時,f(x)=x2﹣4x+3的對稱軸是x=2,∴y=f(x)的值域為[﹣1,3],
下面求g(x)=bx+5﹣2b,x∈[1,4]的值域,
①當b=0時,g(x)=5,不合題意,舍
②當b>0時,g(x)=bx+5﹣2b的值域為[5﹣b,5+2b],只需要 ![]() ,解得b≥6
,解得b≥6
③當b<0時,g(x)=bx+5﹣2b的值域為[5+2b,5﹣b],只需要 ![]() ,解得b≤﹣3
,解得b≤﹣3
綜上:實數b的取值范圍b≥6或b≤﹣3
【解析】(1)根據題意,可以將問題轉化為二次函數對應的方程無實數根,利用△<0列出不等關系式,求解即可得到a的取值范圍;(2)根據二次函數的對稱軸為x=2,可以判斷出二次函數在去甲[﹣1,1]上的單調性,再根據零點的存在性定理列出不等式組,求解即可得到a的取值范圍;(3)根據題意,將問題轉化為函數y=f(x)的值域為函數y=g(x)值域的子集,根據二次函數的性質,即可求得f(x)的值域,對于g(x),對其一次項系數進行分類討論,分別得到g(x)的值域,分別求解,即可得到b的取值范圍.
【考點精析】本題主要考查了二次函數的性質的相關知識點,需要掌握當![]() 時,拋物線開口向上,函數在
時,拋物線開口向上,函數在![]() 上遞減,在
上遞減,在![]() 上遞增;當
上遞增;當![]() 時,拋物線開口向下,函數在
時,拋物線開口向下,函數在![]() 上遞增,在
上遞增,在![]() 上遞減才能正確解答此題.
上遞減才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】某種商品在30天內每件的銷售價格P(元)與時間t(天)的函數關系用下圖的兩條線段表示;該商品在30天內日銷售量Q(件)與時間t(天)之間的關系Q=﹣t+40. 
(1)根據提供的圖象,寫出該商品每件的銷售價格P與時間t的函數關系式;
(2)問這30天內,哪天的銷售額最大,最大是多少?(銷售額=銷售價格×銷售量)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】血藥濃度(Plasma Concentration)是指藥物吸收后在血漿內的總濃度. 藥物在人體內發揮治療作用時,該藥物的血藥濃度應介于最低有效濃度和最低中毒濃度之間.已知成人單次服用1單位某藥物后,體內血藥濃度及相關信息如圖所示:
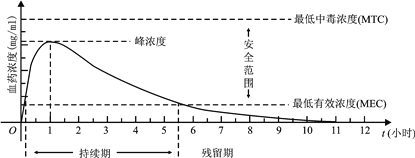
根據圖中提供的信息,下列關于成人使用該藥物的說法中,不正確的個數是
①首次服用該藥物1單位約10分鐘后,藥物發揮治療作用
②每次服用該藥物1單位,兩次服藥間隔小于2小時,一定會產生藥物中毒
③每間隔5.5小時服用該藥物1單位,可使藥物持續發揮治療作用
④首次服用該藥物1單位3小時后,再次服用該藥物1單位,不會發生藥物中毒
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】連擲一枚均勻的骰子兩次,所得向上的點數分別為![]() ,記
,記![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
A. 事件“![]() ”的概率為
”的概率為![]() B. 事件“
B. 事件“![]() 是奇數”與“
是奇數”與“![]() ”互為對立事件
”互為對立事件
C. 事件“![]() ”與“
”與“![]() ”互為互斥事件 D. 事件“
”互為互斥事件 D. 事件“![]() ”的概率為
”的概率為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若一系列函數的解析式和值域相同,但是定義域不同,則稱這些函數為“同族函數”,例如函數y=x2 , x∈[1,2],與函數y=x2 , x∈[﹣2,﹣1]即為“同族函數”.下面的函數解析式也能夠被用來構造“同族函數”的是( )
A.y=x
B.y=|x﹣3|
C.y=2x
D.y=log ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|(x﹣a)[x﹣(a+3)]≤0}(a∈R),B={x|x2﹣4x﹣5>0}.
(1)若A∩B=,求實數a的取值范圍;
(2)若A∪B=B,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com