
【題目】已知定義在R上的奇函數f(x),當x>0時,f(x)=﹣x2+2x
(1)求函數f(x)在R上的解析式;
(2)若函數f(x)在區間[﹣1,a﹣2]上單調遞增,求實數a的取值范圍.
科目:高中數學 來源: 題型:
【題目】連擲一枚均勻的骰子兩次,所得向上的點數分別為![]() ,記
,記![]() ,則下列說法正確的是( )
,則下列說法正確的是( )
A. 事件“![]() ”的概率為
”的概率為![]() B. 事件“
B. 事件“![]() 是奇數”與“
是奇數”與“![]() ”互為對立事件
”互為對立事件
C. 事件“![]() ”與“
”與“![]() ”互為互斥事件 D. 事件“
”互為互斥事件 D. 事件“![]() ”的概率為
”的概率為![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銷售甲、乙兩種商品所得利潤分別是P(萬元)和Q(萬元),它們與投入資金t(萬元)的關系有經驗公式P=3 ![]() ,Q=t.今將3萬元資金投入經營甲、乙兩種商品,其中對甲種商品投資x(萬元).求:
,Q=t.今將3萬元資金投入經營甲、乙兩種商品,其中對甲種商品投資x(萬元).求:
(1)經營甲、乙兩種商品的總利潤y(萬元)關于x的函數表達式;
(2)怎樣將資金分配給甲、乙兩種商品,能使得總利潤y達到最大值,最大值是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={x|(x﹣a)[x﹣(a+3)]≤0}(a∈R),B={x|x2﹣4x﹣5>0}.
(1)若A∩B=,求實數a的取值范圍;
(2)若A∪B=B,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為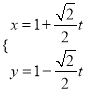 (
(![]() 為參數),在極坐標系(與直角坐標系
為參數),在極坐標系(與直角坐標系![]() 取相同的長度單位,且以原點
取相同的長度單位,且以原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸)中,圓
軸正半軸為極軸)中,圓![]() 的極坐標方程為
的極坐標方程為![]() ,圓
,圓![]() 與直線
與直線![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 點的直角坐標為
點的直角坐標為![]() .
.
(1)將直線![]() 的參數方程化為普通方程,圓
的參數方程化為普通方程,圓![]() 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列各式中,正確的個數是( )
①={0};②{0};③∈{0};④0={0};⑤0∈{0};⑥{1}∈{1,2,3};⑦{1,2}{1,2,3};⑧{a,b}={b,a}.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出以下說法:①不共面的四點中,任意三點不共線;
②有三個不同公共點的兩個平面重合;
③沒有公共點的兩條直線是異面直線;
④分別和兩條異面直線都相交的兩條直線異面;
⑤一條直線和兩條異面直線都相交,則它們可以確定兩個平面.
其中正確結論的序號是_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x﹣1|﹣x,
(1)用分段函數的形式表示該函數,并畫出該函數的圖象;
(2)寫出該函數的值域、單調區間(不要求證明);
(3)若對任意x∈R,不等式|2x﹣1|≥a+x恒成立,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com