
【題目】已知函數f(x)為定義在R上的奇函數,且當x>0時,f(x)=log3x,
(1)求f(x)的解析式;
(2)解不等式f(x)≤2.
【答案】
(1)解:易知f(0)=0;
當x<0時,則﹣x>0,所以f(x)=﹣f(﹣x)=﹣log3(﹣x);
所以f(x)= 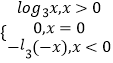
(2)解:由題意:當x>0時有log3x≤2,解得0<x≤9;
當x=0時,f(0)=0顯然滿足題意;
當x<0時有﹣log3(﹣x)≤2,即log3(﹣x)≥﹣2,解得 ![]() .
.
綜上可得原不等式的解集為[0,9] ![]()
【解析】(1)根據函數為奇函數,可設x<0,則﹣x>0,然后將﹣x代入x>0時的解析式化簡即可;(2)按照分段函數分段處理的原則列出不等式,分別解之,最終取并集即可.
【考點精析】掌握函數奇偶性的性質是解答本題的根本,需要知道在公共定義域內,偶函數的加減乘除仍為偶函數;奇函數的加減仍為奇函數;奇數個奇函數的乘除認為奇函數;偶數個奇函數的乘除為偶函數;一奇一偶的乘積是奇函數;復合函數的奇偶性:一個為偶就為偶,兩個為奇才為奇.


科目:高中數學 來源: 題型:
【題目】某網絡營銷部門為了統計某市網友2015年11月11日在某網店的網購情況,隨機抽查了該市100名網友的網購金額情況,得到如下頻率分布直方圖.
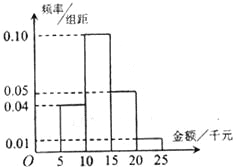
(1)估計直方圖中網購金額的中位數;
(2)若規定網購金額超過15千元的顧客定義為“網購達人”,網購金額不超過15千元的顧客定義為“非網購達人”;若以該網店的頻率估計全市“非網購達人”和“網購達人”的概率,從全市任意選取3人,則3人中“非網購達人”與“網購達人”的人數之差的絕對值為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=loga(ax+1)+mx是偶函數.
(1)求m;
(2)當a>1時,若函數f(x)的圖像與直線l:y=﹣mx+n無公共點,求n的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn . 已知a1=1, ![]() =an+1﹣
=an+1﹣ ![]() n2﹣n﹣
n2﹣n﹣ ![]() ,n∈N* .
,n∈N* .
(1)求數列{an}的通項公式;
(2)設數列{bn}滿足an﹣an﹣1=bna ![]() ,求數列{bn}的n前項和Tn;
,求數列{bn}的n前項和Tn;
(3)是否存在實數λ,使得不等式λa ![]() ﹣
﹣ ![]() +a
+a ![]() +
+ ![]() ≥0恒成立,若存在,求出λ的取值范圍;若不存在,請說明理由.
≥0恒成立,若存在,求出λ的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的短軸長為
的短軸長為![]() ,右焦點為
,右焦點為![]() ,點
,點![]() 是橢圓
是橢圓![]() 上異于左、右頂點
上異于左、右頂點![]() 的一點.
的一點.
(1)求橢圓![]() 的方程;
的方程;
(2)若直線![]() 與直線
與直線![]() 交于點
交于點![]() ,線段
,線段![]() 的中點為
的中點為![]() ,證明:點
,證明:點![]() 關于直線
關于直線![]() 的對稱點在直線
的對稱點在直線![]() 上.
上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=x2+ax+3.
(1)當x∈R時,f(x)≥a恒成立,求a的取值范圍.
(2)當x∈[﹣2,2]時,f(x)≥a恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2 ![]() sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函數f(x)的最小正周期及在區間[0,
sinxcosx+2cos2x﹣1(x∈R) (Ⅰ)求函數f(x)的最小正周期及在區間[0, ![]() ]上的最大值和最小值;
]上的最大值和最小值;
(Ⅱ)若f(x0)= ![]() ,x0∈[
,x0∈[ ![]() ,
, ![]() ],求cos2x0的值.
],求cos2x0的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com