【答案】
分析:(1)根據導數的幾何意義,求出函數f(x)在x=1處的導數值,從而得到切線的斜率,再求出切點坐標,利用直線方程的點斜式列式,化簡成一般式即可得到f(x)在點(1,f(1))處的切線方程;
(2)求出導函數f'(x),分k=0、k<0、0<k<1、k=1、k>1幾種情形,分別在函數的定義域內解不等式f'(x)>0和f'(x)<0,即可得到各種情況下函數的單調區間.
(3)根據(2)的單調性結論,結合函數零點存在性定理可得0<k<1,并由此建立關于k的不等式組,解之即可得到符合題意的實數k的取值范圍.
解答:解:(1)當k=2時,f(x)=ln(1+x)-x+x
2,
∴求導數,得f'(x)=
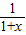
-1+2x,可得f’(1)=

且f(1)=ln2,
∴曲線y=f(x)在點(1,f(1))處的切線方程為y-ln2=

(x-1),化簡得3x-2y+2ln2-3=0;
(2)f'(x)=
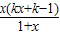
,x∈(-1,+∞)
①當k=0時,f′(x)=-
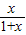
因此,在區間(-1,0)上f'(x)>0;在區間(0,+∞)上f'(x)<0;
∴f(x)的單調遞增區間為(-1,0),單調遞減區間為(0,+∞);
②當k<0時,因為

=
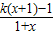
=k+
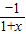
<0
∴若x>0,則f'(x)=
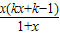
<0;若-1<x<0,則
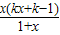
>0
因此,函數f(x)的單調遞增區間為(-1,0),單調遞減區間為(0,+∞);
③當0<k<1時,f′(x)=
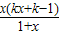
=0,得x
1=0,x
2=
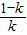
>0;
因此,在區間(-1,0)和(
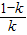
,+∞)上,f'(x)>0;在區間(0,
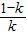
)上,f'(x)<0;
∴函數f(x)的單調遞增區間為(-1,0)和(
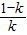
,+∞),單調遞減區間為(0,
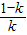
);
④當k=1時,f′(x)=
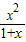
≥0恒成立,故f(x)的遞增區間為(-1,+∞);
⑤當k>1時,由f′(x)=
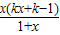
=0,得x
1=0,x
2=
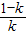
∈(-1,0);
因此,在區間(-1,
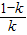
)和(0,+∞)上,f'(x)>0,在區間(
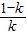
,0)上,f'(x)<0;
∴函數f(x)的單調遞增區間為(-1,
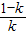
)和(0,+∞),單調遞減區間為(
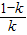
,0).
(3)∵當k>0時,方程f(x)=0 在區間[0,1]有2個不同的根
∴函數f(x)在區間[0,1]的單調性是先增后減,或先減后增
再根據(2)中的單調性,可得0<k<1,且函數f(x)在(0,
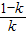
)上為減函數,在(
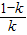
,+∞)上為增函數
∴根據函數零點存在性定理,得
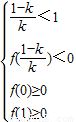
,解之可得2-2ln2≤k<1
即方程f(x)=0 在區間[0,1]有2個不同的根時,實數k的取值范圍為[2-2ln2,1).
點評:本題主要考查了利用導數研究曲線上某點切線方程,以及函數的單調性等知識,屬于中檔題.本題是一道綜合題,還考查運算求解能力、推理論證能力,考查數形結合思想、化歸與轉化思想、分類討論的數學思想等常用的數學知識,是一道不錯的高考題.

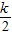 x2
x2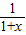 -1+2x,可得f’(1)=
-1+2x,可得f’(1)= 且f(1)=ln2,
且f(1)=ln2, (x-1),化簡得3x-2y+2ln2-3=0;
(x-1),化簡得3x-2y+2ln2-3=0;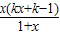 ,x∈(-1,+∞)
,x∈(-1,+∞)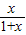
 =
=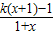 =k+
=k+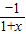 <0
<0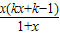 <0;若-1<x<0,則
<0;若-1<x<0,則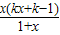 >0
>0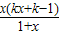 =0,得x1=0,x2=
=0,得x1=0,x2=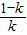 >0;
>0;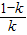 ,+∞)上,f'(x)>0;在區間(0,
,+∞)上,f'(x)>0;在區間(0,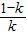 )上,f'(x)<0;
)上,f'(x)<0;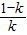 ,+∞),單調遞減區間為(0,
,+∞),單調遞減區間為(0,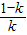 );
);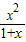 ≥0恒成立,故f(x)的遞增區間為(-1,+∞);
≥0恒成立,故f(x)的遞增區間為(-1,+∞);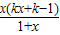 =0,得x1=0,x2=
=0,得x1=0,x2=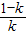 ∈(-1,0);
∈(-1,0);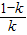 )和(0,+∞)上,f'(x)>0,在區間(
)和(0,+∞)上,f'(x)>0,在區間(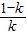 ,0)上,f'(x)<0;
,0)上,f'(x)<0;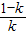 )和(0,+∞),單調遞減區間為(
)和(0,+∞),單調遞減區間為(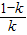 ,0).
,0).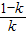 )上為減函數,在(
)上為減函數,在(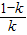 ,+∞)上為增函數
,+∞)上為增函數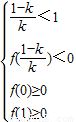 ,解之可得2-2ln2≤k<1
,解之可得2-2ln2≤k<1

