Question

已知函數f（x）=ax³-6ax²+b，問是否存在實數a、b使f（x）在[-1，2]上取得最大值3，最小值-29，若存在，求出a、b的值．并指出函數的單調區間．若不存在，請說明理由．

Answer 1

【答案】分析：要求是否存在a、b使f（x）在[-1，2]上取得最大值3，最小值-29，分兩種情況a＞0，a＜0討論函數的增減性利用導數求閉區間上函數的最值的方法得出a的值即可．
解答：解：a≠0時，f′（x）=3ax²-12ax=3a（x²-4x）
令f′（x）=0，得x=0，或x=4∉[-1，2]（舍）
①a＞0時，如下表

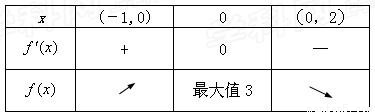
∴當x=0時，f（x）取得最大值，∴b=3；
②a＜0時，如下表

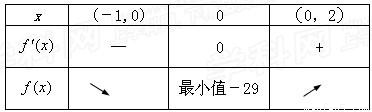
∴當x=0時，f（x）取得最小值，∴b=-29
又f（2）=-16a-29，f（-1）=-7a-29＜f（2）
∴當x=2時，f（x）取得最大值，∴-16a-29=3，a=-2，
綜上：a=2，b=3或a=-2，b=-29．
點評：考查學生利用導數求閉區間上函數的最值的能力．分類討論的數學思想的運用．