若函數y=f(x)在區間[a,b]上是連續的、單調的函數,且滿足f(a)•f(b)<0,則函數y=f(x)在區間[a,b]上有唯一的零點”.對于函數f(x)=-x3+x2+x+m,
(1)當m=0時,討論函數f(x)=-x3+x2+x+m在定義域內的單調性并求出極值;
(2)若函數f(x)=-x3+x2+x+m有三個零點,求實數m的取值范圍.
解:(1)當m=0時,f(x)=-x
3+x
2+x.
∴f′(x)=-3x
2+2x+1=

.
列表如下:

由表可知:函數f(x)=-x
3+x
2+x在區間[-

,1]上單調遞增,在

和(1,+∞)上單調遞減.
∴f(x)的極小值為

=-
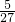
,
極大值為?(1)=1.
(2)由(1)知,當x=-

時,
f(x)取得極小值

,
當x=1時,f(x)取得極大值
f(1)=-1+1+1+m=m+1,
當

,即-1<m<
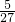
時,
f(-1)=1+1-1+m=m+1>0,

=m-
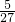
<0,
f(1)=m+1>0,f(2)=m-2<0,
∴f(x)=-x
3+x
2+m在

上有唯一零點.
在

上有唯一零點,在(1,2]上有唯一零點.又f(x)=-x
3+x
2+x+m在(-∞,-1]上單調遞減,
在[2,+∞]上單調遞減,∴在(-∞,-1]上恒有?f(x)≥f(-1)>0,在[2,+∞)上恒有f(x)≤f(2)<0.
∴f(x)=-x
3+x
2+x+m-在(-∞,-1]和[2,+∞)上無零點.∴-1<m<
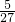
時,函數f(x)=-x
3+x
2+x+m在有三個零點,
∴所求實數m的取值范圍是

.
分析:(1)直接求函數f(x)=-x
3+x
2+x的導函數,判斷單調性求函數極值即可;
(2)三次函數有三個零點,也就是函數圖象與x軸有三個交點,函數的極小值小于0,極大值大于0,即求函數的極值即可解決.
點評:本題考查函數的導數研究函數的單調性,函數零點的概念,以及函數的導數求函數的極值,屬于中檔題.

 .
.
 ,1]上單調遞增,在
,1]上單調遞增,在 和(1,+∞)上單調遞減.
和(1,+∞)上單調遞減. =-
=-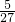 ,
, 時,
時, ,
, ,即-1<m<
,即-1<m<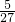 時,
時, =m-
=m-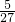 <0,
<0, 上有唯一零點.
上有唯一零點. 上有唯一零點,在(1,2]上有唯一零點.又f(x)=-x3+x2+x+m在(-∞,-1]上單調遞減,
上有唯一零點,在(1,2]上有唯一零點.又f(x)=-x3+x2+x+m在(-∞,-1]上單調遞減,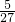 時,函數f(x)=-x3+x2+x+m在有三個零點,
時,函數f(x)=-x3+x2+x+m在有三個零點, .
.
