
分析 (1)cosC=cos(π-A-B)=-cos(A+B)=-cosAcosB+sinAsinB即可求解.
(2)由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sinB}$⇒AC=12$\sqrt{2}$,由D為AB的中點,⇒${\overrightarrow{CD}}^{2}=\frac{1}{4}({\overrightarrow{CA}}^{2}+{\overrightarrow{CB}}^{2}+2\overrightarrow{CA}•\overrightarrow{CB})$=$\frac{1}{4}(288+400+2×12\sqrt{2}×20×(-\frac{\sqrt{2}}{10})$=592,即可求得CD
解答 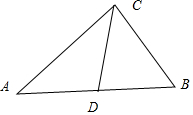 解:(1)在△ABC中,由cosB=$\frac{4}{5}$.得sinB=$\frac{3}{5}$,
解:(1)在△ABC中,由cosB=$\frac{4}{5}$.得sinB=$\frac{3}{5}$,
則cosC=cos(π-A-B)=-cos(A+B)=-cosAcosB+sinAsinB=-$\frac{\sqrt{2}}{2}×\frac{4}{5}+\frac{\sqrt{2}}{2}×\frac{3}{5}=-\frac{\sqrt{2}}{10}$.
(2)在△ABC中,∵sinB=$\frac{3}{5}$,A=45°,BC=20,
由正弦定理得$\frac{BC}{sinA}=\frac{AC}{sinB}$⇒AC=12$\sqrt{2}$,
∵D為AB的中點,∴$\overrightarrow{CD}=\frac{1}{2}(\overrightarrow{CA}+\overrightarrow{CB})$⇒${\overrightarrow{CD}}^{2}=\frac{1}{4}({\overrightarrow{CA}}^{2}+{\overrightarrow{CB}}^{2}+2\overrightarrow{CA}•\overrightarrow{CB})$=$\frac{1}{4}(288+400+2×12\sqrt{2}×20×(-\frac{\sqrt{2}}{10})$=592,
∴CD=4$\sqrt{37}$.
點評 本題考查了三角恒等變形,正弦定理,考查了計算能力,屬于中檔題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | B. | $\frac{1}{3}\overrightarrow a+\frac{2}{3}\overrightarrow b$ | C. | $\frac{1}{3}\overrightarrow a+\frac{1}{3}\overrightarrow b$ | D. | $\frac{1}{2}\overrightarrow a+\frac{1}{2}\overrightarrow b$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{3π}{4}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x2,g(x)=(x+1)2 | ||
| C. | f(x)=x,g(x)=elnx | D. | f(x)=|x|,g(x)=$\left\{\begin{array}{l}{x,}&{x≥0}\\{-x,}&{x<0}\end{array}\right.$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
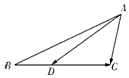 如圖,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC邊上一點,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,則$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值為-2.
如圖,在△ABC中,∠BAC=60°,AB=2,AC=1,D是BC邊上一點,且$\overrightarrow{CD}$=2$\overrightarrow{DB}$,則$\overrightarrow{AD}$•$\overrightarrow{BC}$ 的值為-2.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com