
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() ,當
,當![]() 最大時,求出直線
最大時,求出直線![]() 的直角坐標方程.
的直角坐標方程.
科目:高中數學 來源: 題型:
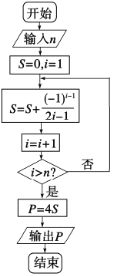
【題目】德國數學家萊布尼茲(1646年-1716年)于1674年得到了第一個關于π的級數展開式,該公式于明朝初年傳入我國.在我國科技水平業已落后的情況下,我國數學家天文學家明安圖(1692年-1765年)為提高我國的數學研究水平,從乾隆初年(1736年)開始,歷時近30年,證明了包括這個公式在內的三個公式,同時求得了展開三角函數和反三角函數的6個新級數公式,著有《割圓密率捷法》一書,為我國用級數計算π開創了先河.如圖所示的程序框圖可以用萊布尼茲“關于π的級數展開式”計算π的近似值(其中P表示π的近似值),若輸入![]() ,則輸出的結果是( )
,則輸出的結果是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修 4-4]參數方程與極坐標系
在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() :
: ![]() ,以平面直角坐標系
,以平面直角坐標系![]() 的原點
的原點![]() 為極點,
為極點, ![]() 軸正半軸為極軸,取相同的單位長度建立極坐標系.已知直線
軸正半軸為極軸,取相同的單位長度建立極坐標系.已知直線 ![]() :
: ![]() .
.
(Ⅰ)試寫出直線![]() 的直角坐標方程和曲線
的直角坐標方程和曲線![]() 的參數方程;
的參數方程;
(Ⅱ)在曲線![]() 上求一點
上求一點![]() ,使點
,使點![]() 到直線
到直線![]() 的距離最大,并求出此最大值.
的距離最大,并求出此最大值.
[選修 4-5]不等式選講
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產的產品中分正品與次品,正品重![]() ,次品重
,次品重![]() ,現有5袋產品(每袋裝有10個產品),已知其中有且只有一袋次品(10個產品均為次品)如果將5袋產品以1~5編號,第
,現有5袋產品(每袋裝有10個產品),已知其中有且只有一袋次品(10個產品均為次品)如果將5袋產品以1~5編號,第![]() 袋取出
袋取出![]() 個產品(
個產品(![]() ),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量
),并將取出的產品一起用秤(可以稱出物體重量的工具)稱出其重量![]() ,若次品所在的袋子的編號是2,此時的重量
,若次品所在的袋子的編號是2,此時的重量![]() _________
_________![]() ;若次品所在的袋子的編號是
;若次品所在的袋子的編號是![]() ,此時的重量
,此時的重量![]() _______
_______![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(13分)編號為A1,A2,…,A16的16名籃球運動員在某次訓練比賽中的得分記錄如下:
運動員編號 | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 | |
得分 | 15 | 35 | 21 | 28 | 25 | 36 | 18 | 34 | |
運動員編號 | A9 | A10 | A11 | A12 | A13 | A14 | A15 | A16 | |
得分 | 17 | 26 | 25 | 33 | 22 | 12 | 31 | 38 |
(Ⅰ)將得分在對應區間內的人數填入相應的空格;
區間 | [10,20) | [20,30) | [30,40] |
人數 |
(Ⅱ)從得分在區間[20,30)內的運動員中隨機抽取2人,
(i)用運動員的編號列出所有可能的抽取結果;
(ii)求這2人得分之和大于50分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】奇函數f(x)在R上存在導數![]() ,當x<0時,
,當x<0時,![]()
![]() f(x),則使得(x2﹣1)f(x)<0成立的x的取值范圍為( )
f(x),則使得(x2﹣1)f(x)<0成立的x的取值范圍為( )
A.(﹣1,0)∪(0,1)B.(﹣∞,﹣1)∪(0,1)
C.(﹣1,0)∪(1,+∞)D.(﹣∞,﹣1)∪(1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓周率是圓的周長與直徑的比值,一般用希臘字母![]() 表示.早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第7位的人,這比歐洲早了約1000年.生活中,我們也可以通過如下隨機模擬試驗來估計
表示.早在公元480年左右,南北朝時期的數學家祖沖之就得出精確到小數點后7位的結果,他是世界上第一個把圓周率的數值計算到小數點后第7位的人,這比歐洲早了約1000年.生活中,我們也可以通過如下隨機模擬試驗來估計![]() 的值:在區間
的值:在區間![]() 內隨機取
內隨機取![]() 個數,構成
個數,構成![]() 個數對
個數對![]() ,設
,設![]() ,
,![]() 能與1構成鈍角三角形三邊的數對
能與1構成鈍角三角形三邊的數對![]() 有
有![]() 對,則通過隨機模擬的方法得到的
對,則通過隨機模擬的方法得到的![]() 的近似值為( )
的近似值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)若![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求函數
垂直,求函數![]() 在
在![]() 點處的切線方程;
點處的切線方程;
(2)若對于![]() ,
,![]() 恒成立,求正實數
恒成立,求正實數![]() 的取值范圍;
的取值范圍;
(3)設函數![]() ,且函數
,且函數![]() 有極大值點
有極大值點![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com