
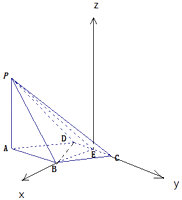
【題目】四棱錐P﹣ABCD的底面ABCD是邊長為1的菱形,∠BCD=60°,E是CD中點,PA⊥底面ABCD,PA=2. 
(1)證明:平面PBE⊥平面PAB;
(2)求直線PC與平面PBE所成的角的正弦值.
【答案】
(1)證明:連結BD,
∵四棱錐P﹣ABCD的底面ABCD是邊長為1的菱形,∠BCD=60°,
∴BD=BC=DC=1,
∵E是CD中點,∴BE⊥DC,
∵AB∥DC,∴BE⊥AB,
∵PA⊥底面ABCD,BE平面ABCD,
∴BE⊥PA,
∵PA∩AB=A,∴BE⊥平面PAB,
∵BE平面PAB,∴平面PBE⊥平面PAB.
(2)解:以E為原點,EB為x軸,EC為y軸,以過點E且垂直于平面ABCD的直線為z軸,
建立空間直角坐標系,
則P( ![]() ,﹣1,2),C(0,
,﹣1,2),C(0, ![]() ,0),B(
,0),B( ![]() ,0,0),E(0,0,0),
,0,0),E(0,0,0),
![]() =(﹣
=(﹣ ![]() ,
, ![]() ,﹣2),
,﹣2), ![]() =(
=( ![]() ,0,0),
,0,0), ![]() =(
=( ![]() ,﹣1,2),
,﹣1,2),
設平面PBE的法向量 ![]() =(x,y,z),
=(x,y,z),
則 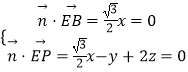 ,取z=1,得
,取z=1,得 ![]() =(0,2,1),
=(0,2,1),
設直線PC與平面PBE所成的角為θ,
則sinθ= 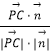 =
= ![]() =
= ![]() .
.
∴直線PC與平面PBE所成的角的正弦值為 ![]() .
.
【解析】(1)連結BD,推導出BE⊥AB,BE⊥PA,從而BE⊥平面PAB,由此能證明平面PBE⊥平面PAB.(2)以E為原點,EB為x軸,EC為y軸,以過點E且垂直于平面ABCD的直線為z軸,建立空間直角坐標系,利用向量法能求出直線PC與平面PBE所成的角的正弦值.
【考點精析】解答此題的關鍵在于理解平面與平面垂直的判定的相關知識,掌握一個平面過另一個平面的垂線,則這兩個平面垂直,以及對空間角的異面直線所成的角的理解,了解已知![]() 為兩異面直線,A,C與B,D分別是
為兩異面直線,A,C與B,D分別是![]() 上的任意兩點,
上的任意兩點,![]() 所成的角為
所成的角為![]() ,則
,則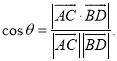 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某食品廠為了檢查甲、乙兩條自動包裝流水線的生產情況,隨機在這兩條流水線上各抽取40件產品作為樣本,并稱出它們的重量(單位:克),重量值落在[495,510)內的產品為合格品,否則為不合格品.統計結果如下:
甲流水線樣本的頻數分布表
產品重量(克) | 頻數 |
[490,495) | 6 |
[495,500) | 8 |
[500,505) | 14 |
[505,510) | 8 |
[510,515] | 4 |
乙流水線樣本的頻率分布直方圖
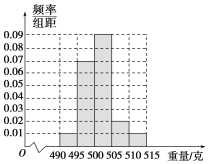
(1)求甲流水線樣本合格的頻率;
(2)由以上統計數據完成下面2×2列聯表,并回答有多大的把握認為產品的包裝質量與兩條自動包裝流水線的選擇有關.
分類 | 甲流水線 | 乙流水線 | 總計 |
合格品 | |||
不合格品 | |||
總計 |
附:K2=![]() .
.
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,在多面體ABCDE中,△BCD是邊長為2的正三角形,AE∥DB,AE⊥DE,2AE=BD,DE=1,面ABDE⊥面BCD,F是CE的中點. 
(Ⅰ)求證:BF⊥CD;
(Ⅱ)求二面角C﹣BF﹣D的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() ,定義域為[0,2π],g(x) 為f(x) 的導函數.
,定義域為[0,2π],g(x) 為f(x) 的導函數.
(1)求方程g(x)=0 的解集;
(2)求函數g(x) 的最大值與最小值;
(3)若函數F(x)=f(x)﹣ax 在定義域上恰有2個極值點,求實數a 的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數f(x)=![]() x3+ax2+5x+6在區間[1,3]上為單調減函數,則實數a的取值范圍是( )
x3+ax2+5x+6在區間[1,3]上為單調減函數,則實數a的取值范圍是( )
A. [﹣![]() ,+∞) B. (﹣∞,﹣3]∪[﹣
,+∞) B. (﹣∞,﹣3]∪[﹣![]() ,+∞)
,+∞)
C. (﹣∞,﹣3] D. [﹣![]() ,
,![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的莖葉圖記錄了甲、乙兩組各5名同學的投籃命中次數,乙組記錄中有一個數據模糊,無法確認,在圖中用![]() 表示.
表示.
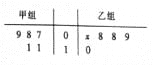
(1)若乙組同學投籃命中次數的平均數比甲組同學的平均數少1,求![]() 及乙組同學投籃命中次數的方差;
及乙組同學投籃命中次數的方差;
(2)在(1)的條件下,分別從甲、乙兩組投籃命中次數低于10次的同學中,各隨機選取一名,求這兩名同學的投籃命中次數之和為16的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4﹣5:不等式選講
設函數f(x)=|2x﹣4|+|x+2|
(1)求函數y=f(x)的最小值;
(2)若不等式f(x)≥|a+4|﹣|a﹣3|恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知p:m∈R,且m+1≤0,q:x∈R,x2+mx+1>0恒成立,若p∧q為假命題且p∨q為真命題,則m的取值范圍是__________________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com