
過點P(2,1)作直線l,與x、y軸的正半軸分別交于A、B兩點,要使|PA|·|PB|最小,求直線l的方程.
x+y-3=0.
解法一:設所求直線l的方程為y-1=k(x-2)(k<0).
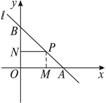
則點A、B的坐標分別為(![]() ,0)和(0,1-2k).
,0)和(0,1-2k).
|PA|=![]()
=-![]() ,|PB|=
,|PB|=![]() .
.
所以|PA|·|PB|=![]() .
.
設![]() =m(*).則2k2+mk+2=0.
=m(*).則2k2+mk+2=0.
因為Δ=m2-16≥0,
所以m≥4或m≤-4.
因為m>0,所以m最小值為4.代入(*)式得
2k2+4k+2=0,即k=-1.
所以所求直線的方程為y-1=-(x-2),
即x+y-3=0.
解法二:由條件k<0,且由解法一得
|PA|·|PB|=![]() .
.
此時![]() ,即k2=1.
,即k2=1.
因為k<0,所以k=-1.
故所求l的方程為y-1=-(x-2),即x+y-3=0.
解法三:設直線l的傾斜角為α,則
|PA|=![]() ,
,![]() .
.
所以|PA|·|PB|=![]() .
.
因為90°<α<180°,
所以當2α=270°,即α=135°時,|PA|·|PB|有最小值.
所以l的方程為y-1=-(x-2),即x+y-3=0.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年四川省成都七中高二(上)10月段考數學試卷(理科)(解析版) 題型:解答題

查看答案和解析>>
科目:高中數學 來源:2012年安徽省淮北市高考數學二模試卷(文科)(解析版) 題型:解答題
 +
+ =1,(a>b>0)與雙曲4x2-
=1,(a>b>0)與雙曲4x2- y2=1有相同的焦點,且橢C的離心e=
y2=1有相同的焦點,且橢C的離心e= ,又A,B為橢圓的左右頂點,M為橢圓上任一點(異于A,B).
,又A,B為橢圓的左右頂點,M為橢圓上任一點(異于A,B).查看答案和解析>>
科目:高中數學 來源:2012年安徽省淮南市高考數學二模試卷(理科)(解析版) 題型:解答題
 +
+ =1,(a>b>0)與雙曲4x2-
=1,(a>b>0)與雙曲4x2- y2=1有相同的焦點,且橢C的離心e=
y2=1有相同的焦點,且橢C的離心e= ,又A,B為橢圓的左右頂點,M為橢圓上任一點(異于A,B).
,又A,B為橢圓的左右頂點,M為橢圓上任一點(異于A,B).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com