
【題目】如圖,四邊形![]() 為矩形,
為矩形,![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,且點
,且點![]() 在
在![]() 上.
上.

(![]() )求證:
)求證:![]() ;
;
(![]() )求三棱錐
)求三棱錐![]() 的體積;
的體積;
(![]() )設點
)設點![]() 在線段
在線段![]() 上,且滿足
上,且滿足![]() ,試在線段
,試在線段![]() 上確定一點
上確定一點![]() ,使得
,使得![]() 平面
平面![]() .
.
【答案】(1)證明見解析;(2)![]() ;(3)當點
;(3)當點![]() 為線段
為線段![]() 上靠近點
上靠近點![]() 的一個三等分.
的一個三等分.
【解析】試題分析:(1)先證明![]() 平面
平面![]() ,得
,得![]() ,由
,由![]() 平面
平面![]() ,得
,得![]() ,從而可得
,從而可得![]() 平面
平面![]() ,由此能證明
,由此能證明![]() ;(2)在
;(2)在![]() 中,過點
中,過點![]() 作
作![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() ,由已知及(
,由已知及(![]() )得
)得![]() ,
,![]() ,從而可得結果;(3)過點
,從而可得結果;(3)過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,過點
,過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,推導出
,推導出![]() 平面
平面![]() ,由此能求出當點
,由此能求出當點![]() 為線段
為線段![]() 上靠近點
上靠近點![]() 的一個三等分點時,
的一個三等分點時,![]() 平面
平面![]() .
.
試題解析:(![]() )證明:由
)證明:由![]() 平面
平面![]() ,
,
及![]() 得
得![]() 平面
平面![]() ,則
,則![]() ,
,
而![]() 平面
平面![]() ,則
,則![]() ,
,
又![]() ,則
,則![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,故
,故![]() .
.
(![]() )在
)在![]() 中,過點
中,過點![]() 作
作![]() 于點
于點![]() ,則
,則![]() 平面
平面![]() .
.
由已知及(![]() )得
)得![]() ,
,![]() .
.
故![]() .
.
(![]() )在
)在![]() 中過點
中過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,
,
在![]() 中過點
中過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() ,
,
則由![]() 得
得![]() ,由平面
,由平面![]()
![]() 平面
平面![]() ,
,
則![]() 平面
平面![]() ,再由
,再由![]() ,
,![]() 得
得![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,則
,則![]() 平面
平面![]() ,
,
故當點![]() 為線段
為線段![]() 上靠近點
上靠近點![]() 的一個三等分點時,
的一個三等分點時,![]() 平面
平面![]() .
.
【方法點晴】本題主要考查線面垂直的判定與性質,以及線面平行的判定定理、利用等積變換求三棱錐體積,屬于難題.證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質,即兩平面平行,在其中一平面內的直線平行于另一平面.


科目:高中數學 來源: 題型:
【題目】(本小題滿分![]() 分)
分)
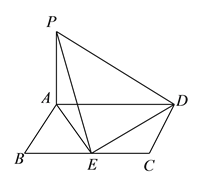
如圖,平行四邊形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,點
,點![]() 為
為![]() 中點,連結
中點,連結![]() 、
、![]() .
.
(Ⅰ)若![]() ,
, ![]() ,求證:平面
,求證:平面![]() 平面
平面![]() .
.
(Ⅱ)若![]() ,試探究在直線
,試探究在直線![]() 上有幾個點
上有幾個點![]() ,使得
,使得![]() ,并說明理由.
,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,矩形ABCD的兩條對角線相交于點M(2,0),AB邊所在直線的方程為x-3y-6=0,點T(-1,1)在AD邊所在直線上.求:

(1) AD邊所在直線的方程;
(2) DC邊所在直線的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校進行體驗,現得到所有男生的身高數據,從中隨機抽取50人進行統計(已知這50個身高介于155 ![]() 到195
到195![]() 之間),現將抽取結果按如下方式分成八組:第一組
之間),現將抽取結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,…,第八組
,…,第八組![]() ,并按此分組繪制如圖所示的頻率分布直方圖,其中第六組
,并按此分組繪制如圖所示的頻率分布直方圖,其中第六組![]() 和第七組
和第七組![]() 還沒有繪制完成,已知第一組與第八組人數相同,第六組和第七組人數的比為5:2.
還沒有繪制完成,已知第一組與第八組人數相同,第六組和第七組人數的比為5:2.
(1)補全頻率分布直方圖;
(2)根據頻率分布直方圖估計這50位男生身高的中位數;
(3)用分層抽樣的方法在身高為![]() 內抽取一個容量為5的樣本,從樣本中任意抽取2位男生,求這兩位男生身高都在
內抽取一個容量為5的樣本,從樣本中任意抽取2位男生,求這兩位男生身高都在![]() 內的概率.
內的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個幾何體的三視圖如圖所示,已知正(主)視圖是底邊長為1的平行四邊形,側(左)視圖是一個長為![]() ,寬為1的矩形,俯視圖為兩個邊長為1的正方形拼成的矩形.
,寬為1的矩形,俯視圖為兩個邊長為1的正方形拼成的矩形.

(1)求該幾何體的體積![]() ;
;
(2)求該幾何體的表面積![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位需要從甲、乙![]() 人中選拔一人參加新崗位培訓,特別組織了
人中選拔一人參加新崗位培訓,特別組織了![]() 個專項的考試,成績統計如下:
個專項的考試,成績統計如下:
第一項 | 第二項 | 第三項 | 第四項 | 第五項 | |
甲的成績 |
|
|
|
|
|
乙的成績 |
|
|
|
|
|
(1)根據有關統計知識,回答問題:若從甲、乙![]() 人中選出
人中選出![]() 人參加新崗培訓,你認為選誰合適,請說明理由;
人參加新崗培訓,你認為選誰合適,請說明理由;
(2)根據有關槪率知識,解答以下問題:
從甲、乙![]() 人的成績中各隨機抽取一個,設抽到甲的成績為
人的成績中各隨機抽取一個,設抽到甲的成績為![]() ,抽到乙的成績為
,抽到乙的成績為![]() ,用
,用![]() 表示滿足條件
表示滿足條件![]() 的事件,求事件
的事件,求事件![]() 的概率.
的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com