Question

2．正三棱柱ABC-A₁B₁C₁的側(cè)棱長為3，AB=4，D是A₁C₁的中點(diǎn)，則AD與面B₁DC所成角的正弦值為$\frac{12}{13}$；點(diǎn)E是BC中點(diǎn)，則過A，D，E三點(diǎn)的截面面積是$\frac{3}{2}\sqrt{30}$．

Answer 1

分析 以A為原點(diǎn)，在平面ABC內(nèi)過A作AC的垂直為x 軸，AC為y軸，AA₁為z軸，建立空間直角坐標(biāo)系，利用向量法能求出AD與面B₁DC所成角的正弦值和過A，D，E三點(diǎn)的截面面積．

解答 解：∵正三棱柱ABC-A₁B₁C₁的側(cè)棱長為3，AB=4，D是A₁C₁的中點(diǎn)，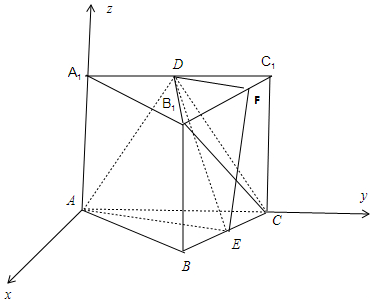
∴以A為原點(diǎn)，在平面ABC內(nèi)過A作AC的垂直為x 軸，AC為y軸，AA₁為z軸，建立空間直角坐標(biāo)系，
A（0，0，0），D（0，2，3），B₁（2$\sqrt{3}$，2，3），C（0，4，0），E（$\sqrt{3}$，3，0），
$\overrightarrow{AD}$=（0，2，3），$\overrightarrow{D{B}_{1}}$=（2$\sqrt{3}$，0，0），$\overrightarrow{DC}$=（0，2，-3），$\overrightarrow{AE}$=（$\sqrt{3}，3，0$），
設(shè)平面B₁DC的法向量$\overrightarrow{n}$=（x，y，z），
則$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{D{B}_{1}}=2\sqrt{3}x=0}\\{\overrightarrow{n}•\overrightarrow{DC}=2y-3z=0}\end{array}\right.$，取z=2，得$\overrightarrow{n}$=（0，3，2），
設(shè)AD與面B₁DC所成角為θ，
則sinθ=$\frac{|\overrightarrow{n}•\overrightarrow{AD}|}{|\overrightarrow{n}|•|\overrightarrow{AD}|}$=$\frac{12}{\sqrt{13}•\sqrt{13}}$=$\frac{12}{13}$．
∴AD與面B₁DC所成角的正弦值為$\frac{12}{13}$；
過D作DF∥AE，交B₁C₁于F，則梯形AEFD就是過A，D，E三點(diǎn)的截面，
∴AE=$\sqrt{16-4}=2\sqrt{3}$，DF=$\frac{1}{2}AE=\sqrt{3}$，
DF到AE的距離d=|$\overrightarrow{AD}$|•$\sqrt{1-（\frac{\overrightarrow{AD}•\overrightarrow{AE}}{|\overrightarrow{AD}|•|\overrightarrow{AE}|}）^{2}}$=$\sqrt{13}$•$\sqrt{\frac{10}{13}}$=$\sqrt{10}$，
∴過A，D，E三點(diǎn)的截面面積是S_梯形AEFD=$\frac{1}{2}$（$\sqrt{3}+2\sqrt{3}$）×$\sqrt{10}$=$\frac{3}{2}\sqrt{30}$．
故答案為：$\frac{12}{13}，\;\frac{3}{2}\sqrt{30}$．

點(diǎn)評 本題考查線面角的正弦值的求法，考查過三點(diǎn)的截面面積的求法，是中檔題，注意向量法的合理運(yùn)用．