
【題目】第十三屆全國人民代表大會第二次會議和政協第十三屆全國委員會第二次會議(簡稱兩會)將分別于![]() 年
年![]() 月
月![]() 日和
日和![]() 月
月![]() 日在北京開幕.全國兩會召開前夕,某網站推出兩會熱點大型調查,調查數據表明,網約車安全問題是百姓最為關心的熱點之一,參與調查者中關注此問題的約占
日在北京開幕.全國兩會召開前夕,某網站推出兩會熱點大型調查,調查數據表明,網約車安全問題是百姓最為關心的熱點之一,參與調查者中關注此問題的約占![]() .現從參與者中隨機選出
.現從參與者中隨機選出![]() 人,并將這
人,并將這![]() 人按年齡分組:第
人按年齡分組:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得到的頻率分布直方圖如圖所示:
,得到的頻率分布直方圖如圖所示:
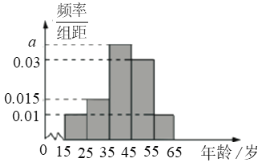
(Ⅰ)現在要從年齡較小的第![]() ,
,![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人贈送禮品,求抽取的
人贈送禮品,求抽取的![]() 人中至少有
人中至少有![]() 人年齡在第
人年齡在第![]() 組的概率;
組的概率;
(Ⅱ)把年齡在第![]() ,
,![]() ,
,![]() 組的人稱為青少年組,年齡在第
組的人稱為青少年組,年齡在第![]() ,
,![]() 組的人稱為中老年組,若選出的
組的人稱為中老年組,若選出的![]() 人中不關注網約車安全問題的人中老年人有
人中不關注網約車安全問題的人中老年人有![]() 人,問是否有
人,問是否有![]() 的把握認為是否關注網約車安全問題與年齡有關?附:
的把握認為是否關注網約車安全問題與年齡有關?附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
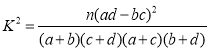 ,
,![]()
【答案】(Ⅰ)![]() ;(Ⅱ)沒有
;(Ⅱ)沒有![]() 的把握認為是否關注網約車安全問題與年齡有關.
的把握認為是否關注網約車安全問題與年齡有關.
【解析】
(Ⅰ)按第1組和第2組的人數,求出抽取5人中從第1組和第2組分別抽取的人數,并按組對抽出的5人進行編號,列出從5人中抽取2人的所有情況,確定2人都在第2組的方法個數,按古典概型概率公式和對立事件的概率關系,即可求解;
(Ⅱ)不關注網約車安全問題的人中老年人有![]() 人,則青年人有
人,則青年人有![]() 人,列出列聯表,根據公式求出
人,列出列聯表,根據公式求出![]() 的觀測值,即可求出結論.
的觀測值,即可求出結論.
(Ⅰ)由頻率直方圖可得第1組和第2組的頻率分別為![]() ,
,
所以第![]() ,
,![]() 組的人數分別為
組的人數分別為![]() ,
,![]() ,
,
從第![]() ,
,![]() 組中用分層抽樣的方法抽取
組中用分層抽樣的方法抽取![]() 人,
人,
則第![]() ,
,![]() 組抽取的人數分別為
組抽取的人數分別為![]() ,
,![]() .
.
抽取的第![]() ,
,![]() 組中
組中![]() 人記為
人記為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所有可能情況為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
全部都在第![]() 組的情況有:
組的情況有:![]() ,
,![]() ,
,![]() ,
,
記從![]() 人中隨機抽取
人中隨機抽取![]() 人,至少有
人,至少有![]() 人年齡在第
人年齡在第![]() 組為事件
組為事件![]() ,
,
則![]() .
.
(Ⅱ)由題意得![]() 列聯表如下:
列聯表如下:
關注網約車安全 | 不關注網約車安全 | 合計 | |
青少年 |
|
|
|
中老年 |
|
|
|
合計 |
|
|
|
![]()
所以沒有![]() 的把握認為是否關注網約車安全問題與年齡有關.
的把握認為是否關注網約車安全問題與年齡有關.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系中,以原點O為極點,x軸的正半軸為極軸建立極坐標系,兩種坐標系中取相同的長度單位.已知直線l的參數方程為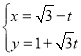 (t為參數),曲線C的極坐標方程為ρ=4sin(θ+
(t為參數),曲線C的極坐標方程為ρ=4sin(θ+![]() ).
).
(1)求直線l的普通方程與曲線C的直角坐標方程;
(2)若直線l與曲線C交于M,N兩點,求△MON的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三陵錐![]() 中,
中,![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,
,![]() 為正三角形,
為正三角形,![]() 為
為![]() 的中點.
的中點.
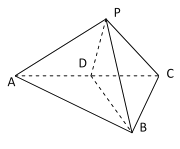
(1)證明:平面![]() 平面
平面![]() ;
;
(2)若二面角![]() 的平面角為銳角,且棱錐
的平面角為銳角,且棱錐![]() 的體積為
的體積為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸正半軸為極軸,建立極坐標系,已知曲線
軸正半軸為極軸,建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】鳳鳴山中學的高中女生體重![]() (單位:kg)與身高
(單位:kg)與身高![]() (單位:cm)具有線性相關關系,根據一組樣本數據
(單位:cm)具有線性相關關系,根據一組樣本數據![]() (
(![]() ),用最小二乘法近似得到回歸直線方程為
),用最小二乘法近似得到回歸直線方程為![]() ,則下列結論中不正確的是( )
,則下列結論中不正確的是( )
A.![]() 與
與![]() 具有正線性相關關系
具有正線性相關關系
B.回歸直線過樣本的中心點![]()
C.若該中學某高中女生身高增加1cm,則其體重約增加0.85kg
D.若該中學某高中女生身高為160cm,則可斷定其體重必為50.29kg.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() :
:![]() ,(t為參數),曲線
,(t為參數),曲線![]() :
:![]() ,(
,(![]() 為參數).
為參數).
(1)以原點為極點,x軸正半軸為極軸建立極坐標系;當![]() 時,求
時,求![]() 與
與![]() 的交點的極坐標(其中極徑
的交點的極坐標(其中極徑![]() ,極角
,極角![]() );
);
(2)過坐標原點O作![]() 的垂線,垂足為A,P為OA中點,當
的垂線,垂足為A,P為OA中點,當![]() 變化時,求P點軌跡的參數方程,并指出它是什么曲線.
變化時,求P點軌跡的參數方程,并指出它是什么曲線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com