
![]() ,側面
,側面![]() 與底面ABC所成的二面角為120°,E、F分別是棱
與底面ABC所成的二面角為120°,E、F分別是棱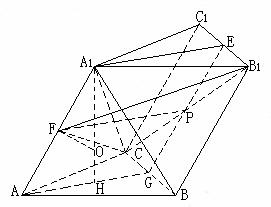 的中點.
的中點.
(Ⅰ)求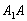 與底面ABC所成的角;
與底面ABC所成的角;
(Ⅱ)證明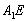 //平面
//平面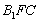 ;
;
(Ⅲ)求經過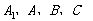 四點的球的體積.
四點的球的體積.
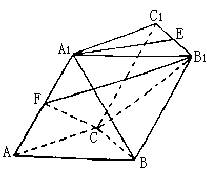
19.(Ⅰ)解:過A1作A1H⊥平面ABC,垂足為H.
連結AH,并延長交BC于G,連結EG,于是∠A1AH為A1A與底面ABC所成的角
 ∵∠A1AB=∠A1AC
∵∠A1AB=∠A1AC
∴AG為∠BAC的平分線。
又∵AB=AC,∴AG⊥BC,且G為BC的中點因此,由三垂線定理,A1A⊥BC
∵A1A∥B1B,且EC∥B1B EC⊥BC,于是∠AGE為二面角A-BC-E的平面角,即
∠AGE=120°
由于四邊形A1AGE為平行四邊形,得
∠A1AG=60°
所以,A1A與底面ABC所成的角為60°。
(Ⅱ)證明:設EG與B1C的交點為P,則點P為EG的中點,連結PF。
在平行四邊形AGEA1中,因F為A1A的中點,故A1E∥FP.
而FP![]() 平面B1FC,A1E
平面B1FC,A1E![]() 平面B1FC,所以A1E∥平面B1FC.
平面B1FC,所以A1E∥平面B1FC.
(Ⅲ)解:連結A1C,在△A1AC和△A1AB中,由于AC=AB, ∠A1AC=∠A1AB,A1A= A1A,則△A1AC≌△A1AB,故A1C=A1B.由已知得
A1A= A1B=A1C=a
又∵A1H⊥平面ABC,∴H為BC的外心.
設所求球的球心為O,則O∈A1H,且球心O與A1A中點的連線OF⊥A1A.
在Rt△A1FO中,
A1O=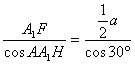 =
=![]() 。
。
故所求球的半徑R=![]() a. 球的體積
a. 球的體積
V=![]() πR3=
πR3=![]() π(
π(![]() a)3=
a)3=![]() πa3。
πa3。


科目:高中數學 來源: 題型:
(05年天津卷)(12分)
如圖,在斜三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,側面
,側面![]() 與底面ABC所成的二面角為120
與底面ABC所成的二面角為120![]() ,E、F分別是棱
,E、F分別是棱![]() 、
、![]() 的中點。
的中點。
(Ⅰ)求![]() 與底面ABC所成的角;
與底面ABC所成的角;
(Ⅱ)證明EA∥平面![]() ;
;
(Ⅲ)求經過![]() 、A、B、C四點的球的體積。
、A、B、C四點的球的體積。

查看答案和解析>>
科目:高中數學 來源:2011-2012學年新疆兵團二中高三第五次月考理科數學試卷(解析版) 題型:解答題
如圖,在斜三棱柱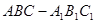 中,點
中,點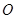 、
、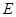 分別是
分別是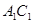 、
、 的中點,
的中點,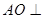 平面
平面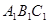 .已知
.已知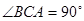 ,
, .
.

(Ⅰ)證明: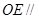 平面
平面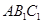 ;
;
(Ⅱ)求異面直線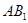 與
與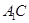 所成的角;
所成的角;
(Ⅲ)求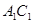 與平面
與平面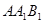 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源:2010年四川省高二下學期期中考試數學卷(文) 題型:選擇題
如圖,在斜三棱柱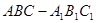 中,
中, ,又
,又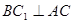 ,過
,過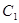 作
作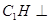 底面
底面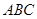 ,垂足為
,垂足為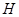 ,則點
,則點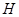 一定在
( )
一定在
( )

A.直線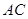 上
B.直線
上
B.直線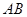 上
上
C.直線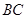 上
D.
上
D.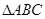 的內部
的內部
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分12分)如圖,在斜三棱柱![]() 中,已知側面
中,已知側面![]() 與底面
與底面![]() 垂直,且
垂直,且![]() ,
,![]() ,
,![]() ,
,![]() .
.
 (Ⅰ)證明:
(Ⅰ)證明:![]() ;
;
(Ⅱ)在平面![]() 內找一點P,使三棱錐
內找一點P,使三棱錐![]() 為正三棱錐(底面為正三角形,頂點在底面內的射影為底面的中心),并求此三棱錐體積.
為正三棱錐(底面為正三角形,頂點在底面內的射影為底面的中心),并求此三棱錐體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com