
已知:如圖,圓錐SO的軸截面是等腰直角三角形,其母線長為4a,A為底面圓周上一點,B是底面圓內一點,且OB⊥AB,C是SA的中點,D是O在SB上的射影.

(Ⅰ)求證:OD⊥平面SAB;
(Ⅱ)設平面SOA和平面SAB所成的二面角為θ(0<θ< ),問能否確定θ,使得三棱錐C—SOD的體積最大?若能,求出體積的最大值和對應的θ;若不能,請說明理由.
),問能否確定θ,使得三棱錐C—SOD的體積最大?若能,求出體積的最大值和對應的θ;若不能,請說明理由.
|
(1)證明 由SO垂直于⊙O所在平面,AB在⊙O內,可得AB⊥SO. ∵AB⊥SO,AB⊥OB,OB 而OD ∴OD⊥AB. 又OD⊥SB,SB ∴OD⊥平面SAB. (2)解 由圓錐SO的軸截面是等腰直角三角形,得OS=OA. 又C是SA的中點,∴OC⊥SA. 由OD⊥平面SAB,OC⊥SA,得DC⊥SA,∠OCD是平面SOA和平面SAB所成的二面角的平面角,則∠OCD=θ. 又∵OC⊥SA,DC⊥SA,OC ∴SA⊥平面COD. 由題意知:△COD是Rt△,且 故得: = 當且僅當OD=CD=
即存在θ= |


科目:高中數學 來源:2015屆福建省高一下學期第一次月考數學試卷(解析版) 題型:解答題
如圖所示,已知在圓錐SO中,底面半徑r=1,母線長l=4,M為母線SA上的一個點,且SM=x,從點M拉一根繩子,圍繞圓錐側面轉到點A,求:

(1)設f(x)為繩子最短長度的平方,求f(x)表達式;
(2)繩子最短時,頂點到繩子的最短距離;
(3)f(x)的最大值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年上海市十校高三(下)第二次聯考數學試卷(文科)(解析版) 題型:解答題
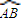 的中點,點P為母線SA的中點.若PQ與SO所成角為
的中點,點P為母線SA的中點.若PQ與SO所成角為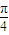 ,求此圓錐的全面積與體積.
,求此圓錐的全面積與體積.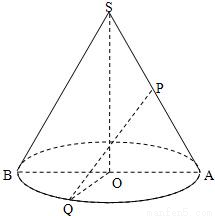
查看答案和解析>>
科目:高中數學 來源:2012年上海市普陀區高三年級第二次質量調研二模理科試卷(解析版) 題型:解答題
如圖,已知圓錐體 的側面積為
的側面積為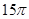 ,底面半徑
,底面半徑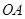 和
和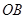 互相垂直,且
互相垂直,且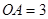 ,
, 是母線
是母線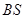 的中點.
的中點.

(1)求圓錐體的體積;
(2)異面直線 與
與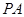 所成角的大小(結果用反三角函數表示).
所成角的大小(結果用反三角函數表示).
【解析】本試題主要考查了圓錐的體積和異面直線的所成的角的大小的求解。
第一問中,由題意, 得
得 ,故
,故
從而體積 .2中取OB中點H,聯結PH,AH.
.2中取OB中點H,聯結PH,AH.
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.在
AH.在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
解:(1)由題意, 得
得 ,
,
故 從而體積
從而體積 .
.
(2)如圖2,取OB中點H,聯結PH,AH.
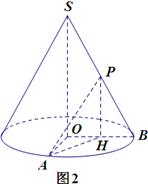
由P是SB的中點知PH//SO,則 (或其補角)就是異面直線SO與PA所成角.
(或其補角)就是異面直線SO與PA所成角.
由SO 平面OAB,
平面OAB, PH
PH 平面OAB,PH
平面OAB,PH AH.
AH.
在 OAH中,由OA
OAH中,由OA OB得
OB得 ;
;
在 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2, ,
,
則 ,所以異面直線SO與P成角的大arctan
,所以異面直線SO與P成角的大arctan
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com