【題目】已知
是定義在區間
內的單調函數，且對任意
，都有
，設
為的導函數，，則函數
的零點個數為（ ）
A. 0 B. 1 C. 2 D. 3
【答案】B
【解析】
設t＝f（x）﹣lnx，則f（x）＝lnx+t，又由f（t）＝e+1，求出f（x）＝lnx+e，從而求出g（x）的解析式，根據函數單調性求出函數的零點個數即可．
對任意的x∈（0，+∞），都有f[f（x）﹣lnx]＝e+1，
又由f（x）是定義在（0，+∞）上的單調函數，則f（x）﹣lnx為定值，
設t＝f（x）﹣lnx，則f（x）＝lnx+t，
又由f（t）＝e+1，即lnt+t＝e+1，解得：t＝e，
則f（x）＝lnx+e，f′（x）＝
＞0，
故g（x）＝lnx+e﹣，則g′（x）＝+
＞0，
故g（x）在（0，+∞）遞增，
而g（1）＝e﹣1＞0，g（
）＝﹣1＜0，
存在x0∈（，1），使得g（x0）＝0，
故函數g（x）有且只有1個零點，
故選：B．
世紀百通期末金卷系列答案科目：高中數學 來源： 題型：
【題目】已知函數
（
，且
）.
（Ⅰ）求函數
的單調區間；
（Ⅱ）求函數
在
上的最大值.
【答案】（Ⅰ）
的單調增區間為
，單調減區間為
.（Ⅱ）當
時， 
；當
時， 
.
【解析】【試題分析】(I)利用
的二階導數來研究求得函數
的單調區間.(II) 由（Ⅰ）得
在
上單調遞減，在
上單調遞增，由此可知
.利用導數和對
分類討論求得函數在
不同取值時的最大值.
【試題解析】
（Ⅰ）
，
設
，則
.
∵
， 
，∴
在
上單調遞增，
從而得
在
上單調遞增，又∵
，
∴當
時， 
，當
時， 
，
因此， 
的單調增區間為
，單調減區間為
.
（Ⅱ）由（Ⅰ）得
在
上單調遞減，在
上單調遞增，
由此可知
.
∵
， 
，
∴
.
設
，
則
.
∵當
時， 
，∴
在
上單調遞增.
又∵
，∴當
時， 
；當
時， 
.
①當
時， 
，即
，這時， 
；
②當
時， 
，即
，這時， 
.
綜上， 
在
上的最大值為：當
時， 
；
當
時， 
.
[點睛]本小題主要考查函數的單調性,考查利用導數求最大值. 與函數零點有關的參數范圍問題，往往利用導數研究函數的單調區間和極值點，并結合特殊點，從而判斷函數的大致圖像，討論其圖象與
軸的位置關系，進而確定參數的取值范圍；或通過對方程等價變形轉化為兩個函數圖象的交點問題．
【題型】解答題
【結束】
22
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，圓
的普通方程為
. 在以坐標原點為極點，
軸正半軸為極軸的極坐標系中，直線
的極坐標方程為
.
（Ⅰ） 寫出圓 的參數方程和直線的直角坐標方程；
（ Ⅱ ） 設直線 與軸和
軸的交點分別為
，
為圓上的任意一點，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）是R上的奇函數，在（0,+
）上是增函數，且f（3）=0,則滿足f（x）>0的實數x的范圍是（ ）
A.（
，3）
（0,3）B.（3,0）（3,+）
C.（，3）（3,+）D.（3,0）（0,3）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數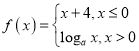
且點
在函數
的圖象上．
（1）求函數的解析式，并在圖中的直角坐標系中畫出函數的圖象；
（2）求不等式
的解集；
（3）若方程
有兩個不相等的實數根，求實數
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝
cos(2x－
)，x∈R.
(1)求函數f(x)的最小正周期和單調遞減區間；
(2)求函數f(x)在區間[－
，
]上的最小值和最大值，并求出取得最值時x的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在創建“全國文明衛生城”過程中，某市“創城辦”為了調查市民對創城工作的了解情況，進行了一次創城知識問卷調查(一位市民只能參加一次).通過隨機抽樣，得到參加問卷調查的1000人的得分(滿分100分)統計結果如下表所示.
組別 |
|
|
|
|
|
|
|
頻數 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
（1）由頻數分布表可以大致認為，此次問卷調查的得分
服從正態分布
， 
近似為這1000人得分的平均值值(同一組數據用該組數據區間的中點值表示)，請用正態分布的知識求
；
（2）在（1）的條件下,“創城辦”為此次參加問卷調查的市民制定如下獎勵方案：:
（ⅰ）得分不低于
的可以獲贈2次隨機話費，得分低于
的可以獲贈1次隨機話費；
（ⅱ）每次獲贈送的隨機話費和對應的概率為：
贈送的隨機話費（單元：元） | 20 | 40 |
概率 | 0.75 | 0.25 |
現有市民甲要參加此次問卷調查，記
(單位：元)為該市民參加問卷調查獲贈的話費,求
的分布列與數學期望.
附：參考數據與公式
，若
，則
①
；
②
；
③
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校
、
兩個班的數學興趣小組在一次數學對抗賽中的成績繪制莖葉圖如下，通過莖葉圖比較兩班數學興趣小組成績的平均值及方差
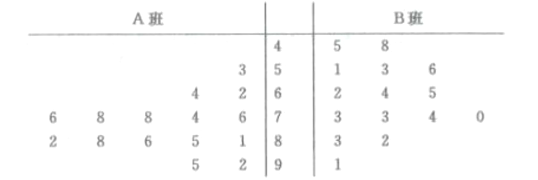
①
班數學興趣小組的平均成績高于
班的平均成績
②
班數學興趣小組的平均成績高于
班的平均成績
③
班數學興趣小組成績的標準差大于
班成績的標準差
④
班數學興趣小組成績的標準差大于
班成績的標準差
其中正確結論的編號為（ ）
A. ①③ B. ①④ C. ②③ D. ②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
