
���}Ŀ���҇�(gu��)�������χ�(y��n)��ȱˮ�ć�(gu��)��֮һ������ȱˮ��(w��n)�}�^��ͻ����ij�О��˹�(ji��)�s������ˮ��Ӌ(j��)���ڱ���ԇ�о���������ˮ���~����(���_��һ��(g��)�����¾���ˮ����(bi��o)��(zh��n)����ˮ�������^(gu��)![]() �IJ��ְ���ƽ�r(ji��)���M(f��i)�����^(gu��)
�IJ��ְ���ƽ�r(ji��)���M(f��i)�����^(gu��)![]() �IJ��ְ����h�r(ji��)���M(f��i))�������^������ش_�����@��(g��)��(bi��o)��(zh��n)��ͨ�^(gu��)��ӫ@����40λ����ij����¾���ˮ��(��λ����)�����շֽM
�IJ��ְ����h�r(ji��)���M(f��i))�������^������ش_�����@��(g��)��(bi��o)��(zh��n)��ͨ�^(gu��)��ӫ@����40λ����ij����¾���ˮ��(��λ����)�����շֽM![]() �������l�ʷֲ�ֱ���D��
�������l�ʷֲ�ֱ���D��
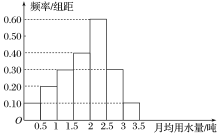
��1�����l�ʷֲ�ֱ���D�й�Ӌ(j��)ԓ40λ�����¾���ˮ���ı���(sh��)����λ��(sh��)��
��2����ԓ�ӱ����¾���ˮ������1���ľ������S�C(j��)��ȡ���ˣ����Ѓ����¾���ˮ����������0.5���ĸ����Ƕ��٣�
���𰸡���1������(sh��)2.25����λ��(sh��)2����2��![]() ��
��
��������
��1������(j��)�l�ʷֲ�ֱ���D�еĔ�(sh��)��(j��)ֱ����⼴��
��2����ֱ���D��֪���¾���ˮ����![]() ���˔�(sh��)��2�ˣ�ӛ��
���˔�(sh��)��2�ˣ�ӛ��![]() ���¾���ˮ����
���¾���ˮ����![]() ���˔�(sh��)��4�ˣ�ӛ��
���˔�(sh��)��4�ˣ�ӛ��![]() ��Ȼ�������e����⼴��.
��Ȼ�������e����⼴��.
��1���ɈD�ɵã�ԓ40λ�����¾���ˮ���ı���(sh��)��2.25��
��?y��n)�ǰ�Ă�(g��)���ε���e���Ξ�![]() ���͞�
���͞�![]()
�������(sh��)��2��
��2����ֱ���D��֪���¾���ˮ����![]() ���˔�(sh��)�飺
���˔�(sh��)�飺![]() �ˣ�ӛ��
�ˣ�ӛ��![]() ��
��
�¾���ˮ����![]() ���˔�(sh��)�飺
���˔�(sh��)�飺![]() �ˣ�ӛ��
�ˣ�ӛ��![]() ��
��
�Ĵ�6�����S�C(j��)��ȡ�������п��ܵ���r�У�
![]() �� ��15�N��
�� ��15�N��
�����¾���ˮ������![]() ����r�У�
����r��![]() ����6�N��
����6�N��
����?x��n)����¾���ˮ���������?/span>0.5���ĸ�����![]() ��
��


 ��У�n��ϵ�д�
��У�n��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ�� ���¹ڷ��������Ӱ��£��ؑc�н�ί푑�(y��ng)��ͣ�n��ͣ�̣�ͣ�n��ͣ�W(xu��)����̖(h��o)���M(j��n)�о�(xi��n)�Ͻ̌W(xu��)��ijУ�����꼉(j��)�ļס��҃ɂ�(g��)���У�����(j��)ij�Δ�(sh��)�W(xu��)�y(c��)ԇ�ɿ�(j��)���x��5���W(xu��)�����Ӕ�(sh��)�W(xu��)��ģ��(j��ng)ِ����֪�@�Μy(c��)ԇ����?n��i)��õijɿ?j��)���o�~�D��D��ʾ�����мװ�5���W(xu��)���ɿ�(j��)��ƽ������83���Ұ�5���W(xu��)���ɿ�(j��)����λ��(sh��)��86.
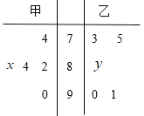
��1�����![]() ��
��![]() ��ֵ���ҷքe��ס��҃ɂ�(g��)����5���W(xu��)���ɿ�(j��)�ķ���
��ֵ���ҷքe��ס��҃ɂ�(g��)����5���W(xu��)���ɿ�(j��)�ķ���![]() ��
��![]() ��������(j��)�Y(ji��)�������J(r��n)�鑪(y��ng)ԓ�x����һ��(g��)��ČW(xu��)�����ӛQِ�����f(shu��)���������.
��������(j��)�Y(ji��)�������J(r��n)�鑪(y��ng)ԓ�x����һ��(g��)��ČW(xu��)�����ӛQِ�����f(shu��)���������.
��2���ijɿ�(j��)?c��)?/span>85�ּ����ϵČW(xu��)�����S�C(j��)��ȡ2������![]() ��ʾ��(l��i)�Լװ���˔�(sh��)�����S�C(j��)׃��X�ķֲ����c��(sh��)�W(xu��)����.
��ʾ��(l��i)�Լװ���˔�(sh��)�����S�C(j��)׃��X�ķֲ����c��(sh��)�W(xu��)����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�ֱ��(xi��n)
�У�ֱ��(xi��n)![]() ��(j��ng)�^(gu��)�c(di��n)
��(j��ng)�^(gu��)�c(di��n)![]() ���Aб�Ǟ�
���Aб�Ǟ�![]() ������(xi��n)
������(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�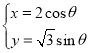 ��
��![]() �酢��(sh��)����������(bi��o)ԭ�c(di��n)
�酢��(sh��)����������(bi��o)ԭ�c(di��n)![]() ��O�c(di��n)����
��O�c(di��n)����![]() �S�������S��O�S�����O����(bi��o)ϵ��
�S�������S��O�S�����O����(bi��o)ϵ��
(1)��(xi��)��ֱ��(xi��n)![]() �ĘO����(bi��o)���̺�����(xi��n)
�ĘO����(bi��o)���̺�����(xi��n)![]() ��ֱ������(bi��o)���̣�
��ֱ������(bi��o)���̣�
(2)�O(sh��)ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �Ľ�����4�����^(gu��)�c(di��n)
�Ľ�����4�����^(gu��)�c(di��n)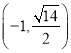 ��
��
��1����E�AE�ķ��̣�
��2���O(sh��)![]() ��
��![]() ��
��![]() ���^(gu��)B�c(di��n)��б�ʞ�
���^(gu��)B�c(di��n)��б�ʞ�![]() ��ֱ��(xi��n)l���E�AE����һ�c(di��n)M����x�S���c(di��n)Q��ֱ��(xi��n)AM�cֱ��(xi��n)
��ֱ��(xi��n)l���E�AE����һ�c(di��n)M����x�S���c(di��n)Q��ֱ��(xi��n)AM�cֱ��(xi��n)![]() �ཻ���c(di��n)P���C����
�ཻ���c(di��n)P���C����![]() ��O������(bi��o)ԭ�c(di��n)����
��O������(bi��o)ԭ�c(di��n)����
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij���S(ch��ng)�����a(ch��n)һ�N���ܹܼ��аl(f��)��һ�_(t��i)���a(ch��n)ԓ���ܹܼ���܇(ch��)����ԓ���ܹܼ��Ѓ�(n��i)��ɂ�(g��)�ڏ����O(ji��n)�ܲ��T(m��n)Ҏ(gu��)�����ڏ��`������Ӌ(j��)�㷽ʽ�飺�ܼ���(n��i)��ɂ�(g��)�ڏ���(sh��)�H�L(zh��ng)�քe��![]() ����(bi��o)��(zh��n)�L(zh��ng)�քe��
����(bi��o)��(zh��n)�L(zh��ng)�քe��![]() �t���ڏ��`������
�t���ڏ��`������![]() ֻҪ���ڏ��`���������^(gu��)
ֻҪ���ڏ��`���������^(gu��)![]() ���J(r��n)��ϸ���֪�@�_(t��i)܇(ch��)���֕�ҹ�ɂ�(g��)��(d��)���������a(ch��n)�����S(ch��ng)�|(zh��)�z���ڃɂ�(g��)�������a(ch��n)�Įa(ch��n)Ʒ�зքe�S�C(j��)��ȡ40������ӱ�����(j��ng)�z�y(c��)���Е����ε�40��(g��)�ӱ�����4��(g��)���ϸ�Ʒ��ҹ���ε�40��(g��)�ӱ�����10��(g��)���ϸ�Ʒ��
���J(r��n)��ϸ���֪�@�_(t��i)܇(ch��)���֕�ҹ�ɂ�(g��)��(d��)���������a(ch��n)�����S(ch��ng)�|(zh��)�z���ڃɂ�(g��)�������a(ch��n)�Įa(ch��n)Ʒ�зքe�S�C(j��)��ȡ40������ӱ�����(j��ng)�z�y(c��)���Е����ε�40��(g��)�ӱ�����4��(g��)���ϸ�Ʒ��ҹ���ε�40��(g��)�ӱ�����10��(g��)���ϸ�Ʒ��
�����������ӱ����l��������ʣ��ڕ�ҹ�ɂ�(g��)�����зքe��ȡ2���a(ch��n)Ʒ��������ǡ��1�����ϸ�a(ch��n)Ʒ�ĸ��ʣ�
������ÿ���θ����a(ch��n)1000������֪ÿ���a(ch��n)Ʒ�ijɱ���5Ԫ��ÿ���ϸ�Ʒ������(r��n)��10Ԫ����(du��)�a(ch��n)Ʒ�z�(y��n)���tÿ���a(ch��n)Ʒ�ęz�(y��n)�M(f��i)�Þ�2.5Ԫ�����в��ϸ�Ʒ�M(j��n)���Ñ�(h��)���У��t���S(ch��ng)Ҫ��(du��)�Ñ�(h��)�r�����@�r(sh��)���a(ch��n)��ÿ�����ϸ�Ʒ���S(ch��ng)Ҫ�pʧ25Ԫ���������ӱ����l��������ʣ��Կ�����(r��n)������ֵ��Q������(j��)�������Ƿ�Ҫ��(du��)ÿ��(g��)���ε����Юa(ch��n)Ʒ���z�y(c��)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��ʾ���������F![]() �У�
��![]() ��
��![]() ��
��![]() ���c(di��n)
���c(di��n)![]() ��
��![]() ���c(di��n)��
���c(di��n)��

��1�����C��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2�����c(di��n)![]() ��
��![]() ���c(di��n)����ƽ��
���c(di��n)����ƽ��![]() �cƽ��
�cƽ��![]() �����J����ǵ�����ֵ��
�����J����ǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() ��?hu��)��タ(xi��n)
��?hu��)��タ(xi��n)![]() �Ľ��c(di��n)����c(di��n)�����x���ʞ�
�Ľ��c(di��n)����c(di��n)�����x���ʞ�![]() .
.
��1����E�A![]() �ķ��̣�
�ķ��̣�
��2����ֱ��(xi��n)![]() �c�E�A
�c�E�A![]() �ཻ��
�ཻ��![]() ��
��![]() ���c(di��n)���cֱ��(xi��n)
���c(di��n)���cֱ��(xi��n)![]() �ཻ��
�ཻ��![]() �c(di��n)��
�c(di��n)��![]() �ǙE�A
�ǙE�A![]() ��һ�c(di��n)�ҝM(m��n)��
��һ�c(di��n)�ҝM(m��n)��![]() ������
������![]() ������(bi��o)ԭ�c(di��n)����ԇ��(w��n)��
������(bi��o)ԭ�c(di��n)����ԇ��(w��n)��![]() �S���Ƿ����һ�c(di��n)
�S���Ƿ����һ�c(di��n)![]() ��ʹ��
��ʹ��![]() �鶨ֵ�������ڣ�����c(di��n)
�鶨ֵ�������ڣ�����c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��ֵ���������ڣ�Ո(q��ng)�f(shu��)������.
��ֵ���������ڣ�Ո(q��ng)�f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������������a(ch��n)��(xi��n)���\(y��n)��Ч�ʣ����S(ch��ng)��(du��)���a(ch��n)��(xi��n)���O(sh��)���M(j��n)���˼��g(sh��)����.���ˌ�(du��)�ȼ��g(sh��)������Ч�����ɼ������a(ch��n)��(xi��n)�ļ��g(sh��)����ǰ���![]() ���B�m(x��)�����\(y��n)�еĕr(sh��)�g�L(zh��ng)�ȣ���λ���죩��(sh��)��(j��)�����L�������o�~�D��
���B�m(x��)�����\(y��n)�еĕr(sh��)�g�L(zh��ng)�ȣ���λ���죩��(sh��)��(j��)�����L�������o�~�D��
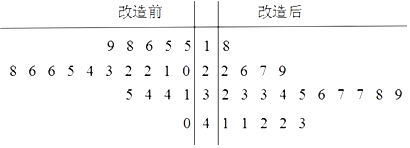
��1�����O(sh��)���ɼ���![]() ��(g��)�B�m(x��)�����\(y��n)�Еr(sh��)�g����λ��(sh��)
��(g��)�B�m(x��)�����\(y��n)�Еr(sh��)�g����λ��(sh��)![]() �������B�m(x��)�����\(y��n)�Еr(sh��)�g���^(gu��)
�������B�m(x��)�����\(y��n)�Еr(sh��)�g���^(gu��)![]() �Ͳ����^(gu��)
�Ͳ����^(gu��)![]() �ĴΔ�(sh��)�����������(li��n)����
�ĴΔ�(sh��)�����������(li��n)����
���^(gu��) | �����^(gu��) | |
����ǰ |
|
|
����� |
|
|
�ڸ���(j��)���е���(li��n)�����ܷ���![]() �İ����J(r��n)�����a(ch��n)��(xi��n)���g(sh��)����ǰ����B�m(x��)�����\(y��n)�Еr(sh��)�g�в��
�İ����J(r��n)�����a(ch��n)��(xi��n)���g(sh��)����ǰ����B�m(x��)�����\(y��n)�Еr(sh��)�g�в��
����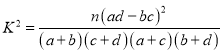 .
.
|
|
|
|
|
|
|
|
��2�����S(ch��ng)�����a(ch��n)��(xi��n)���\(y��n)����Ҫ�M(j��n)�оS�o(h��)�����S(ch��ng)��(du��)���a(ch��n)��(xi��n)�����a(ch��n)�S�o(h��)�M(f��i)�ð��������S�o(h��)�M(f��i)�����ϾS�o(h��)�M(f��i)�ɷN.��(du��)���a(ch��n)��(xi��n)�O(sh��)���S�o(h��)���ڞ�![]() �죨�����_(k��i)���\(y��n)�е���
�죨�����_(k��i)���\(y��n)�е���![]() ��
��![]() �M(j��n)�оS�o(h��).���a(ch��n)��(xi��n)��һ��(g��)���a(ch��n)���ڃ�(n��i)�O(sh��)�Îׂ�(g��)�S�o(h��)���ڣ�ÿ��(g��)�S�o(h��)�������(d��)��.��һ��(g��)�S�o(h��)���ڃ�(n��i)�������a(ch��n)��(xi��n)���B�m(x��)�\(y��n)�У��t����(hu��)�a(ch��n)�����ϾS�o(h��)�M(f��i)�������a(ch��n)��(xi��n)�����B�m(x��)�\(y��n)�У��t�a(ch��n)�����ϾS�o(h��)�M(f��i).��(j��ng)�y(c��)�㣬�����S�o(h��)�M(f��i)��
�M(j��n)�оS�o(h��).���a(ch��n)��(xi��n)��һ��(g��)���a(ch��n)���ڃ�(n��i)�O(sh��)�Îׂ�(g��)�S�o(h��)���ڣ�ÿ��(g��)�S�o(h��)�������(d��)��.��һ��(g��)�S�o(h��)���ڃ�(n��i)�������a(ch��n)��(xi��n)���B�m(x��)�\(y��n)�У��t����(hu��)�a(ch��n)�����ϾS�o(h��)�M(f��i)�������a(ch��n)��(xi��n)�����B�m(x��)�\(y��n)�У��t�a(ch��n)�����ϾS�o(h��)�M(f��i).��(j��ng)�y(c��)�㣬�����S�o(h��)�M(f��i)��![]() �f(w��n)Ԫ/�Σ����ϾS�o(h��)�M(f��i)��һ�Ξ�
�f(w��n)Ԫ/�Σ����ϾS�o(h��)�M(f��i)��һ�Ξ�![]() �f(w��n)Ԫ/���ڣ��˺�ÿ����һ�΄t���ϾS�o(h��)�M(f��i)����
�f(w��n)Ԫ/���ڣ��˺�ÿ����һ�΄t���ϾS�o(h��)�M(f��i)����![]() �f(w��n)Ԫ.�F(xi��n)�ƶ����a(ch��n)��(xi��n)һ��(g��)���a(ch��n)���ڣ���
�f(w��n)Ԫ.�F(xi��n)�ƶ����a(ch��n)��(xi��n)һ��(g��)���a(ch��n)���ڣ���![]() ��Ӌ(j��)����(n��i)�ľS�o(h��)������
��Ӌ(j��)����(n��i)�ľS�o(h��)������![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() .�����a(ch��n)��(xi��n)�ڼ��g(sh��)�����һ��(g��)�S�o(h��)���ڃ�(n��i)���B�m(x��)�����\(y��n)�е��l��������ʣ���һ��(g��)���a(ch��n)���ڃ�(n��i)���a(ch��n)�S�o(h��)�M(f��i)�ķֲ��м�����ֵ.
.�����a(ch��n)��(xi��n)�ڼ��g(sh��)�����һ��(g��)�S�o(h��)���ڃ�(n��i)���B�m(x��)�����\(y��n)�е��l��������ʣ���һ��(g��)���a(ch��n)���ڃ�(n��i)���a(ch��n)�S�o(h��)�M(f��i)�ķֲ��м�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ������(sh��)![]() ��
��
��1����![]() ���{(di��o)�^(q��)�g��
���{(di��o)�^(q��)�g��
��2���ں���(sh��)![]() �ĈD����ȡ
�ĈD����ȡ![]() �ɂ�(g��)��ͬ���c(di��n)����ֱ��(xi��n)
�ɂ�(g��)��ͬ���c(di��n)����ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() ���t�ں���(sh��)�ĈD�����Ƿ�����c(di��n)
���t�ں���(sh��)�ĈD�����Ƿ�����c(di��n)![]() ����
����![]() ��ʹ��
��ʹ��![]() �������ڣ���
�������ڣ���![]() ���c(di��n)������(bi��o)���������ڣ��f(shu��)�����ɣ�
���c(di��n)������(bi��o)���������ڣ��f(shu��)�����ɣ�
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com