【答案】
分析:(1)根據二階行列式的運算分別求得函數f(x)、g(x),分別求出
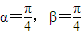
,(x)=f(x)+g(x)和
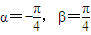
,h(x)=f
2(x)+g
2(x)的解析式,即可判定其奇偶性;
(2)
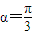
,求出t(x)=f(x)g(x)的解析式,法一:利用積化和差公式,把

化簡為
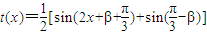
,根據函數為偶函數,即可求得β的值;法2:利用偶函數的定義,可以直接求出β的值;法3:特殊值法,根據函數是偶函數,可得到
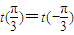
,解此方程即可求得β的值;
(3)根據問題(1)(2)即可以寫出以下結果:寫出任何一種的一個(加法或乘法)均可以.
解答:(理)解:(1)f(x)=sinx-cosα+cosx-cosα,g(x)=cosx•cosα-sinx•sinα
f(x)=sin(x+α),g(x)=cos(x+β)
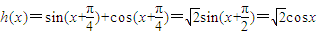
所以h(x)是偶函數
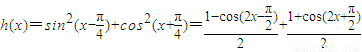
=
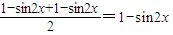
所以h(x)是非奇非偶函數
(2)方法一(積化和差):t(x)=f(x)•g(x)為偶函數,
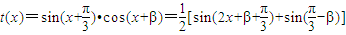
t(x)=f(x)•g(x)為偶函數,所以
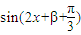
是偶函數,
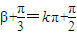
,
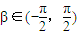
,
∴
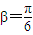
方法二(定義法):t(x)=f(x)•g(x)為偶函數
所以
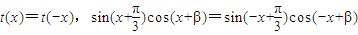
展開整理
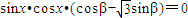
對一切x∈R恒成立
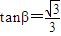
,

,
∴
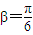
方法三(特殊值法):t(x)=f(x)•g(x)為偶函數
所以
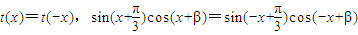
∴
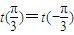
,
所以

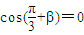
,
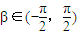
,
∴
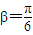
(3)第一層次,寫出任何一種的一個(加法或乘法)均可以,
1、
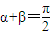
,f(x)+g(x)是偶函數; 2、
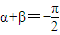
,f(x)+g(x)是奇函數;
3、
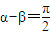
,f(x)+g(x)是非奇非偶函數; 4、
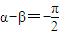
,f(x)+g(x)既奇又偶函數
第二層次,寫出任何一種的一個(加法或乘法)均可以,
1、
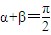
,f
3(x)+g
3(x)是偶函數;(數字不分奇偶)
2、
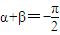
,f
5(x)+g
5(x)是奇函數
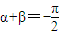
,f
4(x)+g
4(x)是偶函數(數字只能同奇數)
3、
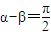
,f
5(x)+g
5(x)是非奇非偶函數(數字不分奇偶,但求相同)
4、
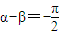
,f
3(x)+g
3(x)是既奇又偶函數 (數字只能奇數)
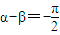
,f
2(x)+g
2(x)是非奇非偶函數
第三層次,寫出逆命題任何一種的一個(加法或乘法)均可以,
1、f
3(x)+g
3(x)是偶函數(數字不分奇偶,但相同),則
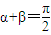
2、f
5(x)+g
5(x)是奇函數(數字只能正奇數),
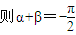
f
2(x)+g
2(x)是偶函數(數字只能正偶數),則
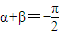
3、f
3(x)+g
3(x)是偶函數 (數字只能正奇數),則

第四層次,寫出充要條件中的任何一種均可以,(16分)
1、
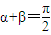
的充要條件是f(x)+g(x)是偶函數
2、f
5(x)+g
5(x)是奇函數(數字只能正奇數)的充要條件是
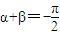
f
2(x)+g
2(x)是偶函數(數字只能正偶數)的充要條件是
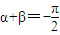
3、f
3(x)+g
3(x)是偶函數 (數字只能正奇數)的充要條件是
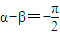
第五層,寫出任何一種均可以(逆命題,充要條件等均可以,限于篇幅省略)
1、
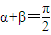
,n∈N
*時,f
n(x)+g
n(x)都是偶函數
2、
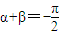
,n∈N
*時,n是正奇數,f
n(x)+g
n(x)是奇函數
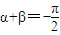
,n∈N
*時,n是正偶數,f
n(x)+g
n(x)是偶函數
3、
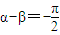
,n∈N
*時,n奇數,f
n(x)+g
n(x)是既奇又偶函數
4、
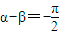
,n∈N
*時,n偶數,f
n(x)+g
n(x)是非奇非偶函數
點評:本題考查函數的奇偶性的判定,題目設置新穎,特別是問題(3)的設置,側重與對于知識的靈活應用,分析、歸納、總結能力的考查,屬中檔題.

 ,
, ,α,β是參數,x∈R,
,α,β是參數,x∈R,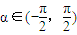 ,
,
 ,判別h(x)=f(x)+g(x)的奇偶性;
,判別h(x)=f(x)+g(x)的奇偶性; ,判別h(x)=f2(x)+g2(x)的奇偶性;
,判別h(x)=f2(x)+g2(x)的奇偶性; ,t(x)=f(x)g(x)是偶函數,求β;
,t(x)=f(x)g(x)是偶函數,求β;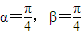 ,(x)=f(x)+g(x)和
,(x)=f(x)+g(x)和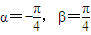 ,h(x)=f2(x)+g2(x)的解析式,即可判定其奇偶性;
,h(x)=f2(x)+g2(x)的解析式,即可判定其奇偶性;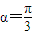 ,求出t(x)=f(x)g(x)的解析式,法一:利用積化和差公式,把
,求出t(x)=f(x)g(x)的解析式,法一:利用積化和差公式,把 化簡為
化簡為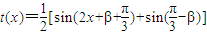 ,根據函數為偶函數,即可求得β的值;法2:利用偶函數的定義,可以直接求出β的值;法3:特殊值法,根據函數是偶函數,可得到
,根據函數為偶函數,即可求得β的值;法2:利用偶函數的定義,可以直接求出β的值;法3:特殊值法,根據函數是偶函數,可得到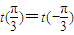 ,解此方程即可求得β的值;
,解此方程即可求得β的值;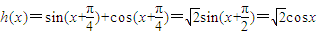
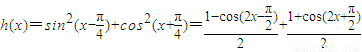
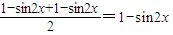
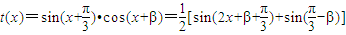
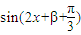 是偶函數,
是偶函數,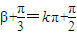 ,
,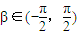 ,
,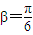
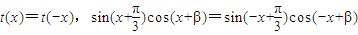
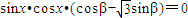 對一切x∈R恒成立
對一切x∈R恒成立 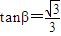 ,
, ,
,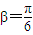
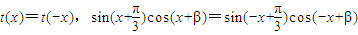
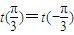 ,
,
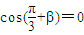 ,
,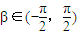 ,
,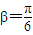
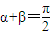 ,f(x)+g(x)是偶函數; 2、
,f(x)+g(x)是偶函數; 2、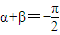 ,f(x)+g(x)是奇函數;
,f(x)+g(x)是奇函數;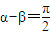 ,f(x)+g(x)是非奇非偶函數; 4、
,f(x)+g(x)是非奇非偶函數; 4、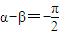 ,f(x)+g(x)既奇又偶函數
,f(x)+g(x)既奇又偶函數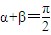 ,f3(x)+g3(x)是偶函數;(數字不分奇偶)
,f3(x)+g3(x)是偶函數;(數字不分奇偶) 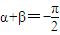 ,f5(x)+g5(x)是奇函數
,f5(x)+g5(x)是奇函數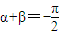 ,f4(x)+g4(x)是偶函數(數字只能同奇數)
,f4(x)+g4(x)是偶函數(數字只能同奇數)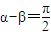 ,f5(x)+g5(x)是非奇非偶函數(數字不分奇偶,但求相同)
,f5(x)+g5(x)是非奇非偶函數(數字不分奇偶,但求相同)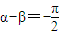 ,f3(x)+g3(x)是既奇又偶函數 (數字只能奇數)
,f3(x)+g3(x)是既奇又偶函數 (數字只能奇數)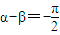 ,f2(x)+g2(x)是非奇非偶函數
,f2(x)+g2(x)是非奇非偶函數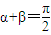
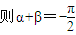
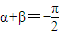

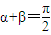 的充要條件是f(x)+g(x)是偶函數
的充要條件是f(x)+g(x)是偶函數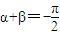
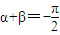
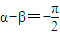
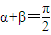 ,n∈N*時,fn(x)+gn(x)都是偶函數
,n∈N*時,fn(x)+gn(x)都是偶函數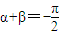 ,n∈N*時,n是正奇數,fn(x)+gn(x)是奇函數
,n∈N*時,n是正奇數,fn(x)+gn(x)是奇函數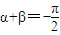 ,n∈N*時,n是正偶數,fn(x)+gn(x)是偶函數
,n∈N*時,n是正偶數,fn(x)+gn(x)是偶函數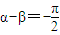 ,n∈N*時,n奇數,fn(x)+gn(x)是既奇又偶函數
,n∈N*時,n奇數,fn(x)+gn(x)是既奇又偶函數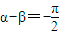 ,n∈N*時,n偶數,fn(x)+gn(x)是非奇非偶函數
,n∈N*時,n偶數,fn(x)+gn(x)是非奇非偶函數
