【題目】已知某摸球游戲的規則如下：從裝有5個大小、形狀完全相同的小球的盒中摸球（其中3個紅球、2個黃球），每次摸一個球記錄顏色并放回，若摸出紅球記1分，摸出黃球記2分．
（1）求“摸球三次得分為5分”的概率；
（2）設ξ為摸球三次所得的分數，求隨機變量ξ的分布列和數學期望．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】如圖，正方體
的棱長為1，E，F分別為棱
，AB上的點，下列說法正確的是________.（填上所有正確命題的序號）
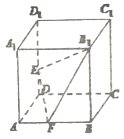
①
平面
②在平面
內總存在與平面平行的直線
③
在側面
上的正投影是面積為定值的三角形
④當E，F為中點時，平面截該正方體所得的截面圖形是五邊形
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知復數
，其中
為虛數單位，對于任意復數
，有
，
．
（1）求
的值；
（2）若復數滿足
，求
的取值范圍；
（3）我們把上述關系式看作復平面上表示復數的點
和表示復數
的點
之間的一個變換，問是否存在一條直線
，若點在直線上，則點仍然在直線上？如果存在，求出直線的方程，否則，說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某單位開展崗前培訓期間，甲、乙2人參加了5次考試，成績統計如下：
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲的成績 | 82 | 82 | 79 | 95 | 87 |
乙的成績 | 95 | 75 | 80 | 90 | 85 |
（1）根據有關統計知識回答問題：若從甲、乙2人中選出1人上崗，你認為選誰合適？請說明理由；
（2）根據有關概率知識解答以下問題：若一次考試兩人成績之差的絕對值不超過3分，則稱該次考試兩人“水平相當”.由上述5次成績統計，任意抽查兩次考試，求至少有一次考試兩人“水平相當”的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為慶祝國慶節，某中學團委組織了“歌頌祖國，愛我中華”知識競賽，從參加考試的學生中抽出60名，將其成績(成績均為整數)分成[40，50)，[50，60)，…，[90，100)六組，并畫出如圖所示的部分頻率分布直方圖，觀察圖形，回答下列問題：
（1）求第四組的頻率，并補全這個頻率分布直方圖；
（2）請根據頻率分布直方圖，估計樣本的眾數、中位數和平均數．（每組數據以區間的中點值為代表）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】運貨卡車以每小時x千米的速度勻速行駛130千米，按交通法規限制50≤x≤100(單位：千米/時).假設汽油的價格是每升2元，而汽車每小時耗油
升，司機的工資是每小時14元.
(1)求這次行車總費用y關于x的表達式；
(2)當x為何值時，這次行車的總費用最低，并求出最低費用的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知點F（2，0），動點P滿足：點P到直線x＝－1的距離比其到點F的距離小1．
（Ⅰ）求點P的軌跡C的方程；
（Ⅱ）過F作直線l垂直于x軸與曲線C交于A、B兩點，Q是曲線C上異于A、B的一點，設曲線C在點A、B、Q處的切線分別為l1、l2、l3，切線l1、l2交于點R，切線l1、l3交于點S，切線l2、l3交于點T，若
RST的面積為6，求Q點的橫坐標．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某二手車直賣網站對其所經營的一款品牌汽車的使用年數x與銷售價格y(單位：萬元，輛)進行了記錄整理，得到如下數據：
(I)畫散點圖可以看出，z與x有很強的線性相關關系，請求出z與x的線性回歸方程(回歸系數
精確到0.01)；
(II)求y關于x的回歸方程，并預測某輛該款汽車當使用年數為10年時售價約為多少．
參考公式：
參考數據：
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
的底面是正方形，每條側棱的長都是底面邊長的
倍，P為側棱SD上的點.
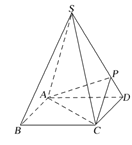
(1)求證：
；
(2)若
平面PAC，則側棱SC上是否存在一點E，使得BE∥平面PAC？若存在，求SE：EC；若不存在，試說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
