操操操操网,久久精品色欧美aⅴ一区二区 ,亚洲成人免费网址

精英家教網 > 高中數學 > 題目詳情

【題目】已知橢圓C：的離心率為，且拋物線的準線恰好過橢圓的一個焦點。

（1）求橢圓C的方程；

（2）過點的直線與橢圓交于兩點，求面積的最大值。

【答案】(1) (2)

【解析】試題分析: （1）設橢圓的焦半距為，拋物線的準線為，

，，代入橢圓的方程即可得答案．

（2）分析易得直線不能與軸垂直，設的方程為，聯立與橢圓的方程得，計算分析可得直線與橢圓有兩個交點，設點，由根與系數的關系分析可得的值，由點到直線的距離公式計算O到l的距離，進而分析可得，由基本不等式的性質分析可得答案．

試題解析:（1）設橢圓的焦半距為，拋物線的準線為，

，所以橢圓的方程是．

（2）由題意直線不能與軸垂直，否則將無法構成三角形．

設其斜率為，那么直線的方程為．

聯立與橢圓的方程，消去，得．

．

設點得，

所以，

又到的距離

所以的面積．

令，那么，

，

因為是減函數

所以當時，所以△OMN面積的最大值是．

練習冊系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導課程推薦,點擊進入>>

相關習題

科目：高中數學 來源： 題型：

【題目】已知橢圓：的上下兩個焦點分別為，，過點與軸垂直的直線交橢圓于、兩點，的面積為，橢圓的離心力為．

（Ⅰ）求橢圓的標準方程；

（Ⅱ）已知為坐標原點，直線：與軸交于點，與橢圓交于，兩個不同的點，若存在實數，使得，求的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】某學校高一年級有學生名，高二年級有學生名.現用分層抽樣方法（按高一年級、高二年級分二層）從該校的學生中抽取名學生，調查他們的數學學習能力.

（Ⅰ）高一年級學生中和高二年級學生中各抽取多少學生？

（Ⅱ）通過一系列的測試，得到這名學生的數學能力值.分別如表一和表二

表一：

高一年級
人數

表二：

高二年級
人數

①確定，并在答題紙上完成頻率分布直方圖；

②分別估計該校高一年級學生和高二年級學生的數學能力值的平均數（同一組中的數據用該組區間的中點值作代表）；

③根據已完成的頻率分布直方圖，指出該校高一年級學生和高二年級學生的數學能力值分布特點的不同之處（不用計算，通過觀察直方圖直接回答結論）

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知f．

（1）如果函數的單調遞減區間為，求函數的解析式；

（2）在（1）的條件下，求函數的圖象在點處的切線方程；

（3）若不等式恒成立，求實數a的取值范圍．

查看答案和解析>>

科目：高中數學 來源： 題型：

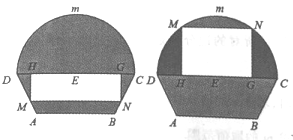
【題目】如圖所示的自動通風設施.該設施的下部是等腰梯形，其中為2米，梯形的高為1米，為3米，上部是個半圓，固定點為的中點. 是由電腦控制可以上下滑動的伸縮橫桿（橫桿面積可忽略不計），且滑動過程中始終保持和平行.當位于下方和上方時，通風窗的形狀均為矩形（陰影部分均不通風）.

（1）設與之間的距離為（且）米，試將通風窗的通風面積（平方米）表示成關于的函數；

（2）當與之間的距離為多少米時，通風窗的通風面積取得最大值？

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知定義在R上的函數f（x）滿足：（1）f（x）+f（2﹣x）=0，（2）f（x﹣2）=f（﹣x），（3）在[﹣1，1]上表達式為f（x）= ，則函數f（x）與函數g（x）= 的圖象區間[﹣3，3]上的交點個數為（）
A.5
B.6
C.7
D.8

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知正項數列{an}的前n項和為Sn ，且滿足4Sn﹣1=an2+2an ， n∈N* ．
（1）求數列{an}的通項公式；
（2）設bn= ，數列{bn}的前n項和為Tn ，證明： ≤Tn＜．

查看答案和解析>>

科目：高中數學 來源： 題型：

【題目】已知向量 =（ sin3x，﹣y）， =（m，cos3x﹣m）（m∈R），且 + = ．設y=f（x）．
（1）求f（x）的表達式，并求函數f（x）在[ ， ]上圖象最低點M的坐標．
（2）在△ABC中，f（A）=﹣ ，且A＞ π，D為邊BC上一點，AC= DC，BD=2DC，且AD=2 ，求線段DC的長．