
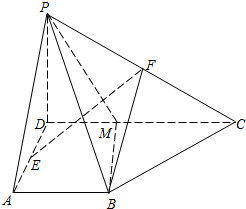
 (理做文不做)如圖,在四棱錐P-ABCD中,PD⊥平面ABCD.底面ABCD為直角梯形,∠BAD=∠ADC=90°,AB=AD=PD=1,CD=3,E,F分別為AD,PC的中點,點M在棱CD上,DM=a.
(理做文不做)如圖,在四棱錐P-ABCD中,PD⊥平面ABCD.底面ABCD為直角梯形,∠BAD=∠ADC=90°,AB=AD=PD=1,CD=3,E,F分別為AD,PC的中點,點M在棱CD上,DM=a.| EF |
| n |
| EF |
| n |
| n |
| EF |
| m |
| v |
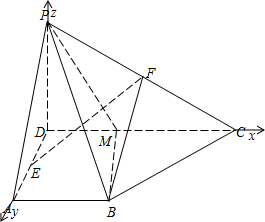 解:(1)如圖建立空間直角坐標系,
解:(1)如圖建立空間直角坐標系,| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| EF |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AP |
| AB |
| n |
|
|
| n |
| n |
| EF |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| EF |
| n |
| BF |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| BF |
|
| ||||
|
|
| ||||||
|
| ||
| 6 |
| ||
| 6 |
| PM |
| PB |
| PC |
| m |
|
|
| m |
| m |
| 14 |
| v |
|
|
| v |
| v |
| 2a2-2a+2 |
| m |
| v |
|
| ||||
|
|
| |5a-1| | ||||
|
| 1 |
| 2 |
| 2 |
| 3 |


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com