
【題目】已知定義在![]() 上的函數
上的函數![]() 為增函數,且
為增函數,且![]() ,則
,則![]() 等于( )
等于( )
A. ![]() B.
B. ![]() C.
C. ![]() 或
或![]() D.
D. ![]()
【答案】A
【解析】
設f(1)=t,由題意知t≠0,令x=1,代入f(x)f[f(x)+![]() ]=1,得f(t+1)=
]=1,得f(t+1)=![]() ,令x=t+1代入f(x)f[f(x)+
,令x=t+1代入f(x)f[f(x)+![]() ]=1,得f(
]=1,得f(![]() +
+![]() )=t=f(1),由在(0,+∞)上的函數f(x)為單調函數,得t2﹣t﹣1=0,由此能求出f(1).
)=t=f(1),由在(0,+∞)上的函數f(x)為單調函數,得t2﹣t﹣1=0,由此能求出f(1).
設f(1)=t,由題意知t≠0,
令x=1,代入f(x)f[f(x)+![]() ]=1,得f(1)f[f(1)+1]=1,
]=1,得f(1)f[f(1)+1]=1,
即f(t+1)=![]() ,
,
令x=t+1代入f(x)f[f(x)+![]() ]=1得,f(t+1)f[f(t+1)+
]=1得,f(t+1)f[f(t+1)+![]() ]=1,
]=1,
∴f(![]() +
+![]() )=t=f(1),
)=t=f(1),
∵在(0,+∞)上的函數f(x)為單調函數,
∴![]() +
+![]() =1,化簡得t2﹣t﹣1=0,
=1,化簡得t2﹣t﹣1=0,
解得,t=![]() 或t=
或t=![]() .
.
∵定義在(0,+∞)上的函數f(x)為增函數,且f(x)f(f(x)+![]() )=1,
)=1,
∴f(1)=![]() .
.
故選:A.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖,正三棱柱![]() 中
中![]() ,
,![]() 為
為![]() 的中點.
的中點.
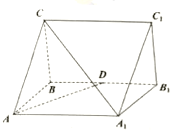
(1)求證:![]() ;
;
(2)若點![]() 為四邊形
為四邊形![]() 內部及其邊界上的點,且三棱錐
內部及其邊界上的點,且三棱錐![]() 的體積為三棱柱
的體積為三棱柱![]() 體積的
體積的![]() ,試在圖中畫出
,試在圖中畫出![]() 點的軌跡,并說明理由.
點的軌跡,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】定義在R上的奇函數y=f(x)滿足f(3)=0,且當x>0時,不等式f(x)>﹣xf′(x)恒成立,則函數g(x)=xf(x)+lg|x+1|的零點的個數為( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數);以原點
為參數);以原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)若把曲線![]() 各點的橫坐標伸長到原來的
各點的橫坐標伸長到原來的![]() 倍,縱坐標變為原來的
倍,縱坐標變為原來的![]() ,得到曲線
,得到曲線![]() ,求曲線
,求曲線![]() 的方程;
的方程;
(Ⅲ)設![]() 為曲線
為曲線![]() 上的動點,求點
上的動點,求點![]() 到曲線
到曲線![]() 上點的距離的最小值,并求此時點
上點的距離的最小值,并求此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓M:: ![]() (a>0)的一個焦點為F(﹣1,0),左右頂點分別為A,B.經過點F的直線l與橢圓M交于C,D兩點.
(a>0)的一個焦點為F(﹣1,0),左右頂點分別為A,B.經過點F的直線l與橢圓M交于C,D兩點.
(1)求橢圓方程;
(2)當直線l的傾斜角為45°時,求線段CD的長;
(3)記△ABD與△ABC的面積分別為S1和S2 , 求|S1﹣S2|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年2月22日,在韓國平昌冬奧會短道速滑男子![]() 米比賽中,中國選手武大靖以連續打破世界紀錄的優異表現,為中國代表隊奪得了本屆冬奧會的首枚金牌,也創造了中國男子冰上競速項目在冬奧會金牌零的突破.根據短道速滑男子
米比賽中,中國選手武大靖以連續打破世界紀錄的優異表現,為中國代表隊奪得了本屆冬奧會的首枚金牌,也創造了中國男子冰上競速項目在冬奧會金牌零的突破.根據短道速滑男子![]() 米的比賽規則,運動員自出發點出發進入滑行階段后,每滑行一圈都要依次經過
米的比賽規則,運動員自出發點出發進入滑行階段后,每滑行一圈都要依次經過![]() 個直道與彎道的交接口
個直道與彎道的交接口![]() .已知某男子速滑運動員順利通過每個交接口的概率均為
.已知某男子速滑運動員順利通過每個交接口的概率均為![]() ,摔倒的概率均為
,摔倒的概率均為![]() .假定運動員只有在摔倒或到達終點時才停止滑行,現在用
.假定運動員只有在摔倒或到達終點時才停止滑行,現在用![]() 表示該運動員滑行最后一圈時在這一圈內已經順利通過的交接口數.
表示該運動員滑行最后一圈時在這一圈內已經順利通過的交接口數.
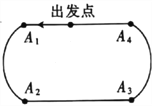
(1)求該運動員停止滑行時恰好已順利通過![]() 個交接口的概率;
個交接口的概率;
(2)求![]() 的分布列及數學期望
的分布列及數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A是拋物線M:y2=2px(p>0)與圓C:x2+(y﹣4)2=a2在第一象限的公共點,且點A到拋物線M焦點F的距離為a,若拋物線M上一動點到其準線與到點C的距離之和的最小值為2a,O為坐標原點,則直線OA被圓C所截得的弦長為( )
A.2
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com