
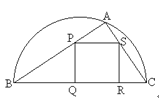
【題目】如圖,某園林單位準備綠化一塊直徑為BC的半圓形空地,△ABC外的地方種草,△ABC的內接正方形PQRS為一水池,其余的地方種花.若BC=a,∠ABC=![]() ,設△ABC的面積為S1,正方形的面積為S2.
,設△ABC的面積為S1,正方形的面積為S2.
(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)當a固定,![]() 變化時,求
變化時,求![]() 取最小值時的角
取最小值時的角![]() .
.
【答案】(1)S1![]() a2sinθcosθ;S2=
a2sinθcosθ;S2=![]() ;(2)當θ
;(2)當θ![]() 時,
時,![]() 的值最小,最小值為
的值最小,最小值為![]() .
.
【解析】
(1)據題三角形ABC為直角三角形,利用三角函數分別求出AC和AB,得出三角形ABC的面積S1;
設正方形PQRS的邊長為x,利用三角函數分別表示出BQ和RC,由BQ+QR+RC=a列出方程求出x,算出S2;
(2)化簡比值![]() ,設t=sin2θ來化簡求出S1與S2的比值,利用三角函數的增減性求出比值的最小值以及對應此時的θ.
,設t=sin2θ來化簡求出S1與S2的比值,利用三角函數的增減性求出比值的最小值以及對應此時的θ.
(1)在Rt△ABC中,AB=acosθ,AC=asinθ,
所以S1![]() ABAC
ABAC![]() a2sinθcosθ;
a2sinθcosθ;
設正方形的邊長為x則BP![]() ,AP=xcosθ,
,AP=xcosθ,
由BP+AP=AB,得![]() xcosθ=acosθ,
xcosθ=acosθ,
解得x![]() ;
;
所以S2=x2![]() ;
;
(2)

![]() sin2θ+1,
sin2θ+1,
令t=sin2θ,因為 0<θ![]() ,
,
所以0<2θ<π,則t=sin2θ∈(0,1],
所以![]() t+1;
t+1;
設g(t)![]() t+1,
t+1,
![]() ,t∈(0,1];
,t∈(0,1];
所以函數g(t)在(0,1]上遞減,
因此當t=1時g(t)有最小值g(t)min=g(1)![]() 1+1
1+1![]() ,
,
此時sin2θ=1,解得θ![]() ;所以當θ
;所以當θ![]() 時,
時,![]() 的值最小,最小值為
的值最小,最小值為![]() .
.


 鴻圖圖書寒假作業假期作業吉林大學出版社系列答案
鴻圖圖書寒假作業假期作業吉林大學出版社系列答案科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,
中,![]() ,不在
,不在![]() 軸上的動點
軸上的動點![]() 滿足
滿足![]() 于點
于點![]() 為
為![]() 的中點。
的中點。
(1)求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)設曲線![]() 與
與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,斜率為
,斜率為![]() 的直線交
的直線交![]() 于
于![]() 兩點,記直線
兩點,記直線![]() 的斜率分別為
的斜率分別為![]() ,試問
,試問![]() 是否為定值?若是,求出該定值;若不是,請說明理由。
是否為定值?若是,求出該定值;若不是,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》節目組決定把《將進酒》、《山居秋暝》、《望岳》、《送杜少府之任蜀州》和另外確定的兩首詩詞排在后六場,并要求《將進酒》與《望岳》相鄰,且《將進酒》排在《望岳》的前面,《山居秋暝》與《送杜少府之任蜀州》不相鄰,且均不排在最后,則后六場開場詩詞的排法有_____________種.(用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小明跟父母、爺爺奶奶一同參加《中國詩詞大會》的現場錄制,5人坐成一排.若小明的父母至少有一人與他相鄰,則不同坐法的總數為
A. 60 B. 72 C. 84 D. 96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,![]() 是圓
是圓![]() 內一個定點,
內一個定點,![]() 是圓上任意一點.線段
是圓上任意一點.線段![]() 的垂直平分線和半徑
的垂直平分線和半徑![]() 相交于點
相交于點![]() .
.
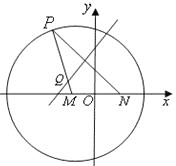
(Ⅰ)當點![]() 在圓上運動時,點
在圓上運動時,點![]() 的軌跡
的軌跡![]() 是什么曲線?并求出其軌跡方程;
是什么曲線?并求出其軌跡方程;
(Ⅱ)過點![]() 作直線
作直線![]() 與曲線
與曲線![]() 交于
交于![]() 、
、![]() 兩點,點
兩點,點![]() 關于原點
關于原點![]() 的對稱點為
的對稱點為![]() ,求
,求![]() 的面積
的面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 為坐標原點,定義非零向量
為坐標原點,定義非零向量![]() ,
,![]() 的“相伴函數”為
的“相伴函數”為![]() ,
,
向量![]()
![]() ,
,![]() 稱為函數
稱為函數![]() 的“相伴向量”.記平面內所有向量的“相伴函數”構成的集合為
的“相伴向量”.記平面內所有向量的“相伴函數”構成的集合為![]() .
.
(1)設函數![]() ,求證:
,求證:![]() ;
;
(2)記![]() ,
,![]() 的“相伴函數”為
的“相伴函數”為![]() ,若函數
,若函數![]() ,
,![]() ,
,![]() 與直線
與直線![]() 有且僅有四個不同的交點,求實數
有且僅有四個不同的交點,求實數![]() 的取值范圍;
的取值范圍;
(3)已知點![]() ,
,![]() 滿足
滿足![]() ,向量
,向量![]() 的“相伴函數”
的“相伴函數”![]() 在
在![]() 處取得最大值.當點
處取得最大值.當點![]() 運動時,求
運動時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某租賃公司擁有汽車100輛,當每輛車的月租金為3200元時,可全部租出。當每輛車的月租金每增加50元時(租金增減為50元的整數倍),未租出的車將會增加一輛。租出的車每輛每月需要維護費150元,未租出的車每輛每月需要維護費50元。
(1)當每輛車的月租金定為3600元時,能租出多少輛車?
(2)設租金為(3200+50x)元/輛(x∈N),用x表示租賃公司的月收益y(單位:元)。
(3)當每輛車的月租金定為多少元時,租賃公司的月收益最大?最大月收益是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面
中,平面![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,△
為正方形,△![]() 為等邊三角形,
為等邊三角形,![]() 是
是![]() 中點,平面
中點,平面![]() 與棱
與棱![]() 交于點
交于點![]() .
.
(Ⅰ)求證:![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(III)記四棱錐![]() 的體積為
的體積為![]() ,四棱錐
,四棱錐![]() 的體積為
的體積為![]() ,直接寫出
,直接寫出![]() 的值.
的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com