
【題目】已知函數![]() .
.
(1)判斷函數![]() 的奇偶性;
的奇偶性;
(2)判斷并證明![]() )在
)在![]() )上的單調性;
)上的單調性;
(3)若![]() 對任意
對任意![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 為奇函數;(2)證明見解析;(3)
為奇函數;(2)證明見解析;(3)![]() .
.
【解析】試題分析:
本題考查函數奇偶性的判斷和單調性的證明,以及根據恒成立問題求參數取值范圍。(1)根據奇偶性的判斷方法證明。(2)根據單調性的判斷方法證明。(3)根據函數的單調性將函數不等式轉化為一般不等式,通過分離參數的方法轉化為求具體函數的最值問題處理。
試題解析:
(1)![]() 定義域R關于原點對稱,
定義域R關于原點對稱,
∵ ,
,
![]() 為奇函數.
為奇函數.
(2)證明:設![]() R,且
R,且![]() ,
,
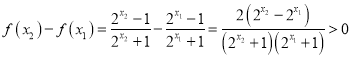 ,
,
∵函數 ![]() 在
在 ![]() 上為增函數,
上為增函數,
![]() ,故
,故![]() ,
,
![]() .
.
∴函數![]() 在
在![]() 上是增函數 .
上是增函數 .
(3)![]()
![]() ,
,
又![]() 為奇函數,
為奇函數,
![]() ,
,
∵![]() 在
在![]() 上是增函數,
上是增函數,
∴![]() 對任意
對任意![]() 恒成立,
恒成立,
∴![]() 對任意
對任意![]() 恒成立,
恒成立,
設![]() ,則
,則![]() ,
,
∵![]() 在
在![]() 上為增函數,
上為增函數,
∴當![]() 時,函數
時,函數![]() 取得最小值,且
取得最小值,且![]() 。
。
∴![]() 。
。
故實數![]() 的取值范圍為
的取值范圍為![]() 。
。


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩人從1,2,…,15這15個數中,依次任取一個數(不放回).則在已知甲取到的數是5的倍數的情況下,甲所取的數大于乙所取的數的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地西紅柿從![]() 月
月![]() 日起開始上市.通過市場調查,得到西紅柿種植成本
日起開始上市.通過市場調查,得到西紅柿種植成本![]() (就是每
(就是每![]() 公斤西紅柿的種植成本,單位:元)與上市時間
公斤西紅柿的種植成本,單位:元)與上市時間![]() (單位:天)的數據如下表:
(單位:天)的數據如下表:
上市時間 | 50 | 110 | 250 |
種植成本 | 150 | 108 | 150 |
(1)根據上表數據,從下列函數中選取一個函數描述西紅柿種植成本與上市時間![]() 的變化關系:
的變化關系:![]() ;
;![]() ;
;![]() ;
;![]() ,并求出函數解析式;
,并求出函數解析式;
(2)利用你選取的函數,求西紅柿種植成本最低時的上市天數及最低種植成本.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線y=﹣x+1與橢圓 ![]() +
+ ![]() =1(a>b>0)相交于A、B兩點.
=1(a>b>0)相交于A、B兩點.
(1)若橢圓的離心率為 ![]() ,焦距為2,求線段AB的長;
,焦距為2,求線段AB的長;
(2)若向量 ![]() 與向量
與向量 ![]() 互相垂直(其中O為坐標原點),當橢圓的離心率e∈[
互相垂直(其中O為坐標原點),當橢圓的離心率e∈[ ![]() ,
, ![]() ]時,求橢圓的長軸長的最大值.
]時,求橢圓的長軸長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , 且滿足a1=1,nSn+1﹣(n+1)Sn= ![]() ,n∈N*
,n∈N*
(1)求a2的值;
(2)求數列{an}的通項公式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】濮陽市黃河灘區某村2010年至2016年人均純收入(單位:萬元)的數據如下表:
年份 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代號x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(Ⅰ)求y關于x的線性回歸方程;
(Ⅱ)利用(Ⅰ)中的回歸方程,分析2010年至2016年該村人均純收入的變化情況,并預測該村2017年人均純收入.
附:回歸直線的斜率和截距的最小乘法估計公式分別為: ![]() =
= 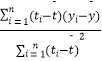 ,
, ![]() =
= ![]() ﹣
﹣ ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知三條直線l1:4x+y-4=0,l2:mx+y=0,l3:2x-3my-4=0.
(1)若直線l1,l2,l3交于一點,求實數m的值;
(2)若直線l1,l2,l3不能圍成三角形,求實數m的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com