
 a>0且a≠1),g(x)是f(x)的反函數.
a>0且a≠1),g(x)是f(x)的反函數. 在區間[2,6]上有實數解,求t的取值范圍;
在區間[2,6]上有實數解,求t的取值范圍; ;
; 時,試比較|
時,試比較| |與4的大小,并說明理由.
|與4的大小,并說明理由. 在[2,6]上有實數解,求出t的表達式,利用導數確定t 的范圍;
在[2,6]上有實數解,求出t的表達式,利用導數確定t 的范圍;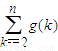 ,利用導數推出是增函數,求出最小值,即可證明
,利用導數推出是增函數,求出最小值,即可證明 ;
; |的取值范圍,最后推出小于4即可.
|的取值范圍,最后推出小于4即可. >0
>0 ,x∈(-∞,-1)∪(1,+∞)
,x∈(-∞,-1)∪(1,+∞) 得t=(x-1)2(7-x),x∈[2,6]
得t=(x-1)2(7-x),x∈[2,6]| x | 2 | (2,5) | 5 | (5,6) | 6 |
| t' | + | - | |||
| t | 5 | 遞增 | 極大值32 | 遞減 | 25 |

 )
)
 =-2lnz+z-
=-2lnz+z- ,z>0
,z>0 =(1-
=(1- )2≥0
)2≥0 >1>0,所以u(
>1>0,所以u( )>u(1)=0
)>u(1)=0 >0
>0 (9分)
(9分)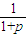 ,則p≥1,1<f(1)=
,則p≥1,1<f(1)= ≤3,
≤3, ≤2<4,
≤2<4,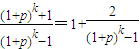 ,
,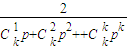
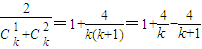 ,
, ≤n-1+
≤n-1+ =n+1-
=n+1- <n+1,
<n+1, <f(1)+n+1≤n+4,
<f(1)+n+1≤n+4,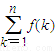 -n|<4.
-n|<4.

 仁愛英語同步練習冊系列答案
仁愛英語同步練習冊系列答案 學習實踐園地系列答案
學習實踐園地系列答案科目:高中數學 來源: 題型:
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
查看答案和解析>>
科目:高中數學 來源:江西省南昌二中2007屆高三數學文科第二次考試卷 題型:044
設a>0且a≠1,f(x)=loga(x+![]() ),(x≥1).
),(x≥1).
(1)求f(x)的反函數f-1(x)和反函數的定義域;
(2)若,f-1(n)<![]() ,求a的取值范圍.
,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com