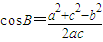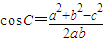在△ABC中,若a2=b2+bc+c2,則A=( )
A.30°
B.60°
C.120°
D.150°
【答案】
分析:本題考查的知識點是余弦定理,觀察到已知條件是“在△ABC中,求A角”,固這應該是一個解三角形問題,又注意到a
2=b
2+bc+c
2給出的三角形三邊的關系,利用余弦定理解題比較恰當.
解答:解:∵a
2=b
2+bc+c
2
∴-bc=b
2+c
2-a
2
由余弦定理的推論得:
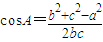
=
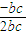
=
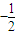
又∵A為三角形內角
∴A=120°
故選C
點評:余弦定理:
a
2=b
2+c
2-2bccosA,
b
2=a
2+c
2-2accosB,
c
2=a
2+b
2-2abcosC.
余弦定理可以變形為: