
【題目】設函數 ![]()
(1)若b和c分別是先后拋擲一枚骰子得到的點數,求對任意x∈R,f(x)>0恒成立的概率.
(2)若b是從區間[0,8](3)任取得一個數,c是從[0,6]任取的一個數,求函數f(x)的圖象與x軸有交點的概率.
【答案】
(1)解:由點(b,c)組成的點共36tkh,
設A={任意x∈R,f(x)>0恒成立}即△=b2﹣c2<0,
∴b<c,A中包含基本事件15個,
∴P(A)= ![]() ;
;
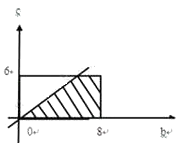
(2)解:(b,c)所在的區域Ω={(b,c)|0≤b≤8,0≤c≤6}
若使函數f(x)的圖象與x軸有交點,
則b≥c≥0.
∴事件B={(b,c)|b>c,0≤b≤8,0≤c≤6}如圖,
∴P(B)= ![]() .
.
【解析】(1)本題是一個等可能事件的概率,試驗發生包含的事件數是6×6=36種結果,f(x)>0要滿足判別式小于0,列舉出結果.(2)利用幾何概型的計算概率的方法解決本題,關鍵要弄準所求的隨機事件發生的區域的面積和事件總體的區域面積,通過相除的方法完成本題的解答.
【考點精析】通過靈活運用幾何概型,掌握幾何概型的特點:1)試驗中所有可能出現的結果(基本事件)有無限多個;2)每個基本事件出現的可能性相等即可以解答此題.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】己知函數f(x)=sinx+ ![]() cosx(x∈R),先將y=f(x)的圖象上所有點的橫坐標縮短到原來的
cosx(x∈R),先將y=f(x)的圖象上所有點的橫坐標縮短到原來的 ![]() 倍(縱坐標不變),再將得到的圖象上所有點向右平行移動θ(θ>0)個單位長度,得到的圖象關于直線x=
倍(縱坐標不變),再將得到的圖象上所有點向右平行移動θ(θ>0)個單位長度,得到的圖象關于直線x= ![]() 對稱,則θ的最小值為( )
對稱,則θ的最小值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若![]() 沿著三條中位線折起后能夠拼接成一個三棱錐,則稱這樣的
沿著三條中位線折起后能夠拼接成一個三棱錐,則稱這樣的![]() 為“和諧三角形”,設
為“和諧三角形”,設![]() 的三個內角分別為
的三個內角分別為![]() ,
, ![]() ,
, ![]() ,則下列條件不能夠確定為“和諧三角形”的是
,則下列條件不能夠確定為“和諧三角形”的是![]()
A. ![]() ; B.
; B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某城市100戶居民的月平均用電量(單位:度),以[160,180),[180,200),[200,200),[220.240),
[240,260),[260,280),[280,300)分組的頻率分布直方圖如圖.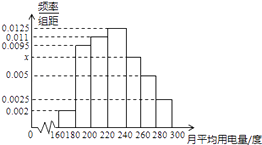
(1)求直方圖中x的值;
(2)在月平均用電量為,[220,240),[240,260),[260,280)的三用戶中,用分層抽樣的方法抽取10居民,則月平均用電量在[220,240)的用戶中應抽取多少戶?
(3)求月平均用電量的中位數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C1: ![]() +
+ ![]() =1(a>b>0)過點A(1,
=1(a>b>0)過點A(1, ![]() ),其焦距為2.
),其焦距為2. 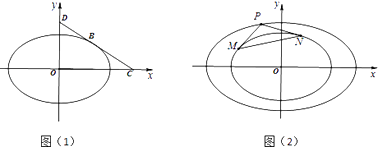
(1)求橢圓C1的方程;
(2)已知橢圓具有如下性質:若橢圓的方程為 ![]() +
+ ![]() =1(a>b>0),則橢圓在其上一點A(x0 , y0)處的切線方程為
=1(a>b>0),則橢圓在其上一點A(x0 , y0)處的切線方程為 ![]() +
+ ![]() =1,試運用該性質解決以下問題:
=1,試運用該性質解決以下問題:
(i)如圖(1),點B為C1在第一象限中的任意一點,過B作C1的切線l,l分別與x軸和y軸的正半軸交于C,D兩點,求△OCD面積的最小值;
(ii)如圖(2),過橢圓C2: ![]() +
+ ![]() =1上任意一點P作C1的兩條切線PM和PN,切點分別為M,N.當點P在橢圓C2上運動時,是否存在定圓恒與直線MN相切?若存在,求出圓的方程;若不存在,請說明理由.
=1上任意一點P作C1的兩條切線PM和PN,切點分別為M,N.當點P在橢圓C2上運動時,是否存在定圓恒與直線MN相切?若存在,求出圓的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是定義在R上的不恒為零的函數,且對于任意實數x,y滿足:f(2)=2,f(xy)=xf(y)+yf(x),an= ![]() (n∈N*),bn=
(n∈N*),bn= ![]() (n∈N*),考查下列結論:
(n∈N*),考查下列結論:
①f(1)=1;②f(x)為奇函數;③數列{an}為等差數列;④數列{bn}為等比數列.
以上命題正確的是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某蔬菜商店買進的土豆![]() (噸)與出售天數
(噸)與出售天數![]() (天)之間的關系如下表所示:
(天)之間的關系如下表所示:
| 2 | 3 | 4 | 5 | 6 | 7 | 9 | 12 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(1)請根據上表數據在所給網格紙中繪制散點圖;
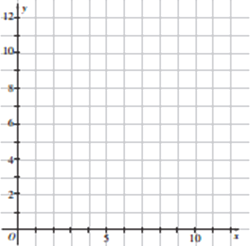
(2)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() (其中
(其中![]() 保留2位有效數字);
保留2位有效數字);
(3)根據(2)中的計算結果,若該蔬菜商店買進土豆40噸,則預計可以銷售多少天(計算結果保留整數)?
附:  ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列{an}的首項為8,Sn是其前n項的和,某同學經計算得S2=20,S3=36,S4=65,后來該同學發現了其中一個數算錯了,則該數為( )
A.S1
B.S2
C.S3
D.S4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com