
【題目】以![]() 為直徑的圓上每一點都染上了紅、黃、藍三色之一,已知
為直徑的圓上每一點都染上了紅、黃、藍三色之一,已知![]() 、
、![]() 染上了紅色,聯結圓上的點組成三角形,給出4個結論:
染上了紅色,聯結圓上的點組成三角形,給出4個結論:
①必定存在一個直角三角形,三個頂點同為紅色;
②必定存在一個直角三角形,三個頂點同色;
③必定存在一個直角三角形,三個頂點全不同色;
④必定存在一個直角三角形,或都三個頂點同色,或者三個頂點全不同色。
則真命題的個數是( )個。
A. 1 B. 2
C. 3 D. 4
【答案】A
【解析】
易知,聯結圓上的點組成直角三角形,當且僅當斜邊為直徑,下面討論直徑.若除點![]() 、
、![]() 外,圓上再無紅點,則結論①不成立;若除點
外,圓上再無紅點,則結論①不成立;若除點![]() 、
、![]() 外,圓上再無紅點,且其他所有直徑的兩端點都黃、藍異色,則結論②不成立;若圓上所有直徑的兩端點都同色,則結論③不成立.下面證明:結論④成立.若除點
外,圓上再無紅點,且其他所有直徑的兩端點都黃、藍異色,則結論②不成立;若圓上所有直徑的兩端點都同色,則結論③不成立.下面證明:結論④成立.若除點![]() 、
、![]() 外,圓上還有紅點,則存在三個頂點同色的直角三角形(同紅色),命題成立,若除點
外,圓上還有紅點,則存在三個頂點同色的直角三角形(同紅色),命題成立,若除點![]() 、
、![]() 外,圓上再無紅點(即圓上其余點染上了黃、藍兩色之一),則作直徑
外,圓上再無紅點(即圓上其余點染上了黃、藍兩色之一),則作直徑![]() ,當
,當![]() 兩端異色時,存在三個頂點全不同色的直角三角形,命題成立;當
兩端異色時,存在三個頂點全不同色的直角三角形,命題成立;當![]() 兩端同色時,不妨記為同黃色,若此時圓上還有第三個黃點,則存在三個頂點同黃色的直角三角形,命題成立.若此時圓上沒有第三個黃點,即除點
兩端同色時,不妨記為同黃色,若此時圓上還有第三個黃點,則存在三個頂點同黃色的直角三角形,命題成立.若此時圓上沒有第三個黃點,即除點![]() 、
、![]() 、
、![]() 、
、![]() 外圓上全為藍點,則存在三個頂點同藍色的直角三角形,命題成立。綜上得結論④成立。
外圓上全為藍點,則存在三個頂點同藍色的直角三角形,命題成立。綜上得結論④成立。


科目:高中數學 來源: 題型:
【題目】某次數學測驗共有12道選擇題,每道題共有四個選項,且其中只有一個選項是正確的,評分標準規定:每選對1道題得5分,不選或選錯得0分. 在這次數學測驗中,考生甲每道選擇題都按照規則作答,并能確定其中有9道題能選對;其余3道題無法確定正確選項,在這3道題中,恰有2道能排除兩個錯誤選項,另1題只能排除一個錯誤選項. 若考生甲做這3道題時,每道題都從不能排除的選項中隨機挑選一個選項作答,且各題作答互不影響.在本次測驗中,考生甲選擇題所得的分數記為![]()
(1)求![]() 的概率;
的概率;
(2)求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有6人參加某娛樂活動,該活動有甲、乙兩個游戲可供參加者選擇,為增加趣味性,主辦方制作了一款電腦軟件:按下電腦鍵盤“![]() ”鍵則會出現模擬拋兩枚質地均勻的骰子的畫面,若干秒后在屏幕上出現兩個點數
”鍵則會出現模擬拋兩枚質地均勻的骰子的畫面,若干秒后在屏幕上出現兩個點數![]() 和
和![]() ,并在屏幕的下方計算出
,并在屏幕的下方計算出![]() 的值.主辦方現規定:每個人去按“
的值.主辦方現規定:每個人去按“![]() ”鍵,當顯示出來的
”鍵,當顯示出來的![]() 小于
小于![]() 時則參加甲游戲,否則參加乙游戲.
時則參加甲游戲,否則參加乙游戲.
(1)求這6個人中恰有2人參加甲游戲的概率;
(2)用![]() 、
、![]() 分別表示這6個人中去參加甲,乙游戲的人數,記
分別表示這6個人中去參加甲,乙游戲的人數,記![]() ,求隨機變量
,求隨機變量![]() 的分布列與數學期望
的分布列與數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]()
![]() 的右頂點
的右頂點![]() ,離心率為
,離心率為![]() ,
,![]() 為坐標原點.
為坐標原點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)已知![]() (異于點
(異于點![]() )為橢圓
)為橢圓![]() 上一個動點,過
上一個動點,過![]() 作線段
作線段![]() 的垂線
的垂線![]() 交橢圓
交橢圓![]() 于點
于點![]() ,求
,求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,為保護河上古橋OA,規劃建一座新橋BC,同時設立一個圓形保護區.規劃要求:新橋BC與河岸AB垂直;保護區的邊界為圓心M在線段OA上并與BC相切的圓,且古橋兩端O和A到該圓上任意一點的距離均不少于80 m.經測量,點A位于點O正北方向60 m處,點C位于點O正東方向170 m處(OC為河岸),tan∠BCO=![]() .
.

(1)求新橋BC的長;
(2)當OM多長時,圓形保護區的面積最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() (
(![]() )的左、右焦點分別為
)的左、右焦點分別為![]() ,過點
,過點![]() 的直線
的直線![]() 交
交![]() 于
于![]() ,
,![]() 兩點,
兩點,![]() 的周長為
的周長為![]() ,
, ![]() 的離心率
的離心率![]()
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)設點![]() ,
,![]() ,過點
,過點![]() 作
作![]() 軸的垂線
軸的垂線![]() ,試判斷直線
,試判斷直線![]() 與直線
與直線![]() 的交點是否恒在一條定直線上?若是,求該定直線的方程;否則,說明理由.
的交點是否恒在一條定直線上?若是,求該定直線的方程;否則,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查觀眾對電影“復仇者聯盟4”結局的滿意程度,研究人員在某電影院隨機抽取了1000名觀眾作調查,所得結果如下所示,其中不喜歡“復仇者聯盟4”的結局的觀眾占被調查觀眾總數的![]() .
.
男性觀眾 | 女性觀眾 | 總計 | |
喜歡“復仇者聯盟4”的結局 | 400 | ||
不喜歡“復仇者聯盟4”的結局 | 200 | ||
總計 |
(Ⅰ)完善上述![]() 列聯表;
列聯表;
(Ⅱ)是否有99.9%的把握認為觀眾對電影“復仇者聯盟4”結局的滿意程度與性別具有相關性?
附: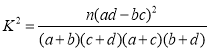
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com