Question

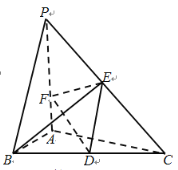
【題目】如圖，在三棱錐P-ABC中，底面ABC，，，，D，E分別為棱BC，PC的中點，點F在棱PA上，設．

（1）當時，求異面直線DF與BE所成角的余弦值；

（2）試確定t的值，使二面角C-EF-D的平面角的余弦值為．

Answer 1

【答案】（1）；（2）或．

【解析】

（1）建立空間直角坐標系，寫出的坐標，利用向量夾角公式求異面直線的角即可；

（2）設，，利用向量求出二面角的余弦，得出或，即可知的值.

在三棱錐中，底面ABC，，

則，，

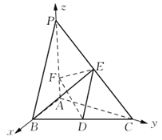
故以基底，建立如圖所示的空間直角坐標系，

因為，，

所以，，，．

因為D，E分別為棱BC，PC的中點，

所以，．

（1）當時，．

所以．

設異面直線DF與BE所成的角為，

則，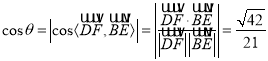

所以異面直線DF與BE所成角的余弦值為．

（2）設，，

則，．

因為，，，

平面APC，所以平面APC，

故平面CEF的一個法向量為．

設平面DEF的一個法向量為，

則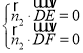，即．

不妨取，則，，

所以平面DEF的一個法向量為．

因為二面角的平面角的余弦值為，

所以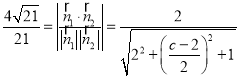

解得或，

則或．

因此，當或時，

二面角的平面角的余弦值為．