
【題目】已知函數f(x)=alnx+x2+bx(a為實常數).
(1)若a=﹣2,b=﹣3,求f(x)的單調區間;
(2)若b=0,且a>﹣2e2 , 求函數f(x)在[1,e]上的最小值及相應的x值;
(3)設b=0,若存在x∈[1,e],使得f(x)≤(a+2)x成立,求實數a的取值范圍.
【答案】
(1)解:a=﹣2,b=﹣3時,f(x)=﹣2lnx+x2﹣3x,定義域為(0,+∞),
![]() ,
,
在(0,+∞)上,f′(2)=0,當x∈(0,2)時,f′(x)<0,當x∈(2,+∞)時,f′(x)>0,
所以函數f(x)的單調增區間為(2,+∞);單調減區間為(0,2);
(2)解:因為b=0,所以f(x)=alnx+x2 ![]() ,
,
x∈[1,e],2x2+a∈[a+2,a+2e2],
(i) 若a≥﹣2,f'(x)在[1,e]上非負(僅當a=﹣2,x=1時,f'(x)=0),
故函數f(x)在[1,e]上是增函數,
此時[f(x)]min=f(1)=1;
(ii)若﹣2e2<a<﹣2,a+2<0,a+2e2>0,
![]() ,x∈[1,e],
,x∈[1,e],
當 ![]() 時,f'(x)=0,
時,f'(x)=0, ![]() ,
,
當 ![]() 時,f'(x)<0,此時f(x)是減函數;
時,f'(x)<0,此時f(x)是減函數;
當 ![]() 時,f'(x)>0,此時f(x)是增函數.
時,f'(x)>0,此時f(x)是增函數.
故 ![]() ;
;
(3)解:b=0,f(x)=alnx+x2不等式f(x)≤(a+2)x,
即alnx+x2≤(a+2)x可化為a(x﹣lnx)≥x2﹣2x.
因為x∈[1,e],所以lnx≤1≤x且等號不能同時取,
所以lnx<x,即x﹣lnx>0,因而 ![]() (x∈[1,e]),
(x∈[1,e]),
令 ![]() (x∈[1,e]),又
(x∈[1,e]),又 ![]() ,
,
當x∈[1,e]時,x﹣1≥0,lnx≤1,x+2﹣2lnx>0,
從而g'(x)≥0(僅當x=1時取等號),所以g(x)在[1,e]上為增函數,
故g(x)的最小值為g(1)=﹣1,所以實數a的取值范圍是[﹣1,+∞)
【解析】(1)求出函數的導數,解關于導函數的不等式,求出函數的單調區間即可;(2)求出函數的導數,通過討論a的范圍,求出函數的單調區間,從而求出函數的最小值即可;(3)問題轉化為 ![]() (x∈[1,e]),令
(x∈[1,e]),令 ![]() (x∈[1,e]),根據函數的單調性求出a的范圍即可.
(x∈[1,e]),根據函數的單調性求出a的范圍即可.
【考點精析】掌握利用導數研究函數的單調性和函數的最大(小)值與導數是解答本題的根本,需要知道一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減;求函數
在這個區間單調遞減;求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值.
比較,其中最大的是一個最大值,最小的是最小值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知定義在(0,+∞)上的連續函數y=f(x)滿足:xf′(x)﹣f(x)=xex且f(1)=﹣3,f(2)=0.則函數y=f(x)( )
A.有極小值,無極大值
B.有極大值,無極小值
C.既有極小值又有極大值
D.既無極小值又無極大值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從高三抽出![]() 名學生參加數學競賽,由成績得到如下的頻率分布直方圖.試利用頻率分布直方圖求:
名學生參加數學競賽,由成績得到如下的頻率分布直方圖.試利用頻率分布直方圖求:
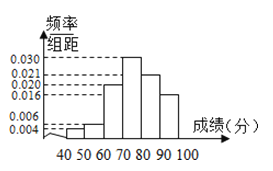
(1)這![]() 名學生成績的眾數與中位數;
名學生成績的眾數與中位數;
(2)這![]() 名學生的平均成績.
名學生的平均成績.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以原點為極點,
為參數),在以原點為極點, ![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的傾斜角;
的傾斜角;
(2)設點![]() ,直線
,直線![]() 和曲線
和曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設甲、乙、丙三個乒乓球協會分別選派3,1,2名運動員參加某次比賽,甲協會運動員編號分別為![]() ,
,![]() ,
,![]() ,乙協會編號為
,乙協會編號為![]() ,丙協會編號分別為
,丙協會編號分別為![]() ,
,![]() ,若從這6名運動員中隨機抽取2名參加雙打比賽.
,若從這6名運動員中隨機抽取2名參加雙打比賽.
(1)用所給編號列出所有可能抽取的結果;
(2)求丙協會至少有一名運動員參加雙打比賽的概率;
(3)求參加雙打比賽的兩名運動員來自同一協會的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 是兩條不同的直線,
是兩條不同的直線,![]() 是三個不同的平面,給出下列四個命題:①若
是三個不同的平面,給出下列四個命題:①若![]() ,則
,則![]() ; ②若
; ②若![]() 則
則![]() ;③若
;③若![]() ,則
,則![]() ; ④若
; ④若![]() ,則
,則![]() ,其中正確命題的序號是( )
,其中正確命題的序號是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了實現綠色發展,避免浪費能源,某市政府計劃對居民用電采用階梯收費的方法.為此,相關部分在該市隨機調查了![]() 戶居民六月份的用電量(單位:
戶居民六月份的用電量(單位:![]() )和家庭收入(單位:萬元),以了解這個城市家庭用電量的情況.
)和家庭收入(單位:萬元),以了解這個城市家庭用電量的情況.
用電量數據如下:
![]() .
.
對應的家庭收入數據如下:
![]()
![]() .
.
(Ⅰ)根據國家發改委的指示精神,該市計劃實施![]() 階階梯電價,使
階階梯電價,使![]() 的用戶在第一檔,電價為
的用戶在第一檔,電價為![]() 元/
元/![]() ;
;![]() 的用戶在第二檔,電價為
的用戶在第二檔,電價為![]() 元/
元/![]() ;
;![]() 的用戶在第三檔,電價為
的用戶在第三檔,電價為![]() 元/
元/![]() ,試求出居民用電費用
,試求出居民用電費用![]() 與用電量
與用電量![]() 間的函數關系;
間的函數關系;
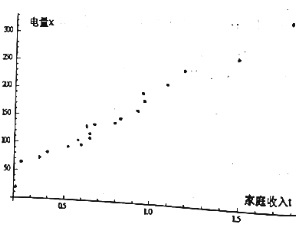
(Ⅱ)以家庭收入![]() 為橫坐標,電量
為橫坐標,電量![]() 為縱坐標作出散點圖(如圖),求
為縱坐標作出散點圖(如圖),求![]() 關于
關于![]() 的回歸直線方程(回歸直線方程的系數四舍五入保留整數).
的回歸直線方程(回歸直線方程的系數四舍五入保留整數).
(Ⅲ)小明家的月收入![]() 元,按上述關系,估計小明家月支出電費多少元?
元,按上述關系,估計小明家月支出電費多少元?
參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
參考公式:一組相關數據![]() ,
,![]() ,…,
,…,![]() 的回歸直線方程
的回歸直線方程![]() 的斜率和截距的最小二乘法估計分別為
的斜率和截距的最小二乘法估計分別為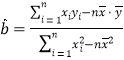 ,
,![]() ,其中
,其中![]() ,
,![]() 為樣本均值.
為樣本均值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com