
已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當![]() 時,求函數(shù)f(x)的最小值;
時,求函數(shù)f(x)的最小值;
(2)設函數(shù)h(x)=(1-x)f(x)+16,試根據(jù)m的取值分析函數(shù)h(x)的圖象與函數(shù)g(x)的圖象交點的個數(shù).
(1) x=4時,取等號,故函數(shù)f(x)的最小值為0.
(2)當![]() 或
或![]() 時,h(x)的圖象與g(x)的圖象恰有1個交點;
時,h(x)的圖象與g(x)的圖象恰有1個交點;
當![]() 時,h(x)的圖象與g(x)的圖象恰有2個交點;
時,h(x)的圖象與g(x)的圖象恰有2個交點;
當![]() 時,h(x)的圖象與g(x(的圖象恰有3個交點.
時,h(x)的圖象與g(x(的圖象恰有3個交點.
(1) 方法一: ∵ x>1 , ![]() ,
,
當且僅當x=4時,取等號,故函數(shù)f(x)的最小值為0;
方法二:∵ x>1, ![]()
當且僅當![]() 即x=4時,取等號,故函數(shù)f(x)的最小值為0.
即x=4時,取等號,故函數(shù)f(x)的最小值為0.
方法三:求導(略) ……………………………………4分
(2)由于h(x)=(1-x)f(x)+16=![]()
設 F(x)=g(x)-h(huán)(x)= ![]() (
(![]() 且
且![]() ),則
),則
![]() ,……………………………6分
,……………………………6分
令![]() 得x=3或x=1(舍)又∵
得x=3或x=1(舍)又∵![]() ,
,![]() ,
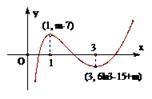
,![]() ,F(xiàn)(3)=6ln3-15+m
,F(xiàn)(3)=6ln3-15+m
根據(jù)導數(shù)的符號及函數(shù)的單調(diào)情況、取極值的情況作出的草圖如下:………………11分
由此可得:
當![]() 或
或![]() 時,h(x)的圖象與g(x)的圖象恰有1個交點;
時,h(x)的圖象與g(x)的圖象恰有1個交點;
當![]() 時,h(x)的圖象與g(x)的圖象恰有2個交點;
時,h(x)的圖象與g(x)的圖象恰有2個交點;
當![]() 時,h(x)的圖象與g(x(的圖象恰有3個交點.
時,h(x)的圖象與g(x(的圖象恰有3個交點.


 孟建平錯題本系列答案
孟建平錯題本系列答案 超能學典應用題題卡系列答案
超能學典應用題題卡系列答案科目:高中數(shù)學 來源: 題型:
| a |
| x |
| 1 |
| x |
| 4 |
| x |
| b2 |
| x |
| 8 |
| x |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 已知函數(shù)f(x)的定義域為[-2,+∞),部分對應值如表格所示,f′(x)為f(x).的導函數(shù),函數(shù)y=f′(x)的圖象如右圖所示: 已知函數(shù)f(x)的定義域為[-2,+∞),部分對應值如表格所示,f′(x)為f(x).的導函數(shù),函數(shù)y=f′(x)的圖象如右圖所示:
|
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com