
【題目】【2017屆河北省正定中學高三上學期第三次月考(期中)數學(理)】在平面直角坐標系中,當![]() 不是原點時,定義
不是原點時,定義![]() 的“伴隨點”為
的“伴隨點”為![]() ;當
;當![]() 是原點時,定義
是原點時,定義![]() 的“伴隨點”為它自身,平面曲線
的“伴隨點”為它自身,平面曲線![]() 上所有點的“伴隨點”所構成的曲線
上所有點的“伴隨點”所構成的曲線![]() 定義為曲線
定義為曲線![]() 的“伴隨曲線”,現有下列命題:
的“伴隨曲線”,現有下列命題:
①若點![]() 的“伴隨點”是點
的“伴隨點”是點![]() ,則點
,則點![]() 的“伴隨點”是點
的“伴隨點”是點![]() ;
;
②若曲線![]() 關于
關于![]() 軸對稱,則其“伴隨曲線”
軸對稱,則其“伴隨曲線” ![]() 關于
關于![]() 軸對稱;
軸對稱;
③單位圓的“伴隨曲線”是它自身;
④一條直線的“伴隨曲線”是一條直線.
其中真命題的個數為( )
A. 1 B. 2 C. 3 D. 4
 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案科目:高中數學 來源: 題型:
【題目】性格色彩學創始人樂嘉是江蘇電視臺當紅節目“非誠勿擾”的特約嘉賓,他的點評視角獨特,語言犀利,給觀眾留下了深刻的印象,某報社為了了解觀眾對樂嘉的喜愛程度,隨機調查了觀看了該節目的140名觀眾,得到如下的列聯表:(單位:名)
男 | 女 | 總計 | ||||||
喜愛 | 40 | 60 | 100 | |||||
不喜愛 | 20 | 20 | 40 | |||||
總計 | 60 | 80 | 140 | |||||
p(k2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | |||
k0 | 2.705 | 3.841 | 5.024 | 6.635 | 7.879 | |||
(Ⅰ)從這60名男觀眾中按對樂嘉是否喜愛采取分層抽樣,抽取一個容量為6的樣本,問樣本中喜愛與不喜愛的觀眾各有多少名?
(Ⅱ)根據以上列聯表,問能否在犯錯誤的概率不超過0.025的前提下認為觀眾性別與喜愛樂嘉有關?(精確到0.001)
(Ⅲ)從(Ⅰ)中的6名男性觀眾中隨機選取兩名作跟蹤調查,求選到的兩名觀眾都喜愛樂嘉的概率.
附: 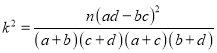
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]() ,其中
,其中![]() ,
, ![]() ,
, ![]() 為自然對數的底數.
為自然對數的底數.
(Ⅰ)若![]() 和
和![]() 在區間
在區間![]() 內具有相同的單調性,求實數
內具有相同的單調性,求實數![]() 的取值范圍;
的取值范圍;
(Ⅱ)若![]() ,且函數
,且函數![]() 的最小值為
的最小值為![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義域為R的函數![]() 是奇函數
是奇函數
(1)求![]() 的值
的值
(2)判斷f(x)在![]() 上的單調性。(直接寫出答案,不用證明)
上的單調性。(直接寫出答案,不用證明)
(3)若對于任意![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2016高考四川文科】已知數列{![]() }的首項為1,
}的首項為1,![]() 為數列
為數列![]() 的前n項和,
的前n項和,![]() ,其中q>0,
,其中q>0,![]() .
.
(Ⅰ)若![]() 成等差數列,求
成等差數列,求![]() 的通項公式;
的通項公式;
(Ⅱ)設雙曲線![]() 的離心率為
的離心率為![]() ,且
,且![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】羅源濱海新城建一座橋,兩端的橋墩已建好,這兩墩相距![]() 米,余下工程只需建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為32萬元,距離為x米的相鄰兩墩之間的橋面工程費用為
米,余下工程只需建兩端橋墩之間的橋面和橋墩,經預測,一個橋墩的工程費用為32萬元,距離為x米的相鄰兩墩之間的橋面工程費用為![]() 萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為
萬元.假設橋墩等距離分布,所有橋墩都視為點,且不考慮其他因素,記余下工程的費用為![]() 萬元.
萬元.
(1)試寫出![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)當![]() =96米,需新建多少個橋墩才能使余下工程的費用
=96米,需新建多少個橋墩才能使余下工程的費用![]() 最小?
最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在區間
在區間![]() 上為單調遞增函數,求
上為單調遞增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() 且
且![]() ,又
,又![]() 是
是![]() 的導函數.若正常數
的導函數.若正常數![]() 滿足條件
滿足條件![]() .證明:
.證明: ![]() <0.
<0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com