
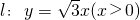 上,A,B兩點關于x軸對稱,O為坐標原點,且線段AB上有一點M滿足|AM|•|MB|=3.當點A在l上移動時,記點M的軌跡為W.
上,A,B兩點關于x軸對稱,O為坐標原點,且線段AB上有一點M滿足|AM|•|MB|=3.當點A在l上移動時,記點M的軌跡為W.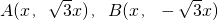 ,
,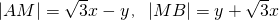 ,
,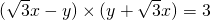 ,即
,即 ,
,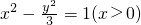 .
.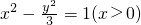 關于x軸對稱,
關于x軸對稱,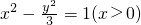 上,所以x0≥1.
上,所以x0≥1.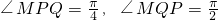 ,則∠MQP=2∠MPQ;
,則∠MQP=2∠MPQ;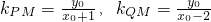 ,
,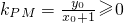 ,且
,且 ,
,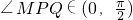 ,且
,且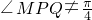 ,
,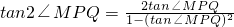 =
=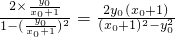 ,
,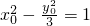 ,即y02=3x02-3,
,即y02=3x02-3,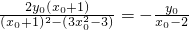 ,
,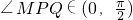 ,且
,且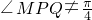 ,∠MQP∈(0,π),
,∠MQP∈(0,π),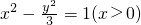 關于x軸對稱,所以只要證明“點M在x軸上方及x軸上時,∠MQP=2∠MPQ”成立即可.
關于x軸對稱,所以只要證明“點M在x軸上方及x軸上時,∠MQP=2∠MPQ”成立即可.

 新思維假期作業寒假吉林大學出版社系列答案
新思維假期作業寒假吉林大學出版社系列答案科目:高中數學 來源: 題型:
| 3 |
| OP |
| OQ |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
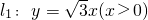 上,A,B兩點關于x軸對稱,O為坐標原點,且線段AB上有一點M滿足|AM|•|MB|=3.當點A在l1上移動時,記點M的軌跡為W.
上,A,B兩點關于x軸對稱,O為坐標原點,且線段AB上有一點M滿足|AM|•|MB|=3.當點A在l1上移動時,記點M的軌跡為W.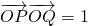 .
.查看答案和解析>>
科目:高中數學 來源:西城區二模 題型:解答題
| 3 |
| OP |
| OQ |
查看答案和解析>>
科目:高中數學 來源:2009年北京市西城區高考數學二模試卷(文科)(解析版) 題型:解答題
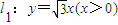 上,A,B兩點關于x軸對稱,O為坐標原點,且線段AB上有一點M滿足|AM|•|MB|=3.當點A在l1上移動時,記點M的軌跡為W.
上,A,B兩點關于x軸對稱,O為坐標原點,且線段AB上有一點M滿足|AM|•|MB|=3.當點A在l1上移動時,記點M的軌跡為W.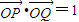 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com